��Ŀ����
����Ŀ����ͼ1����![]() ��������
��������![]() �ĶԽ���
�ĶԽ���![]() �ϣ�������
�ϣ�������![]() �ı߳���
�ı߳���![]() ��
��![]() ������ֱ�DZ�
������ֱ�DZ�![]() �ֱ�
�ֱ�![]() �ڵ�
�ڵ�![]() ��
��
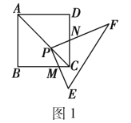
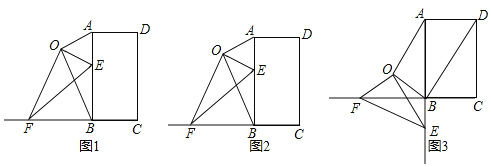
��1���������֣���ͼ2���̶���![]() ��ʹ
��ʹ![]() �Ƶ�
�Ƶ�![]() ��ת����
��ת����![]() ʱ���ı���
ʱ���ı���![]() �������Σ�
��������
��գ��ٵ�![]() ʱ���ı���
ʱ���ı���![]() �ı߳���_____��
�ı߳���_____��
�ڵ�![]() ��
��![]() ����ʵ����ʱ���ı���
����ʵ����ʱ���ı���![]() �������______��
�������______��
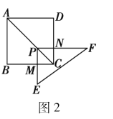
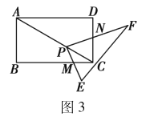
��2��������֤����ͼ3�����ı���![]() ����״�ı�Ϊ���Σ�
����״�ı�Ϊ���Σ�![]() ��
��![]() ����
����![]() �ھ���
�ھ���![]() �ĶԽ���
�ĶԽ���![]() ��
��![]() ������ֱ�DZ�
������ֱ�DZ�![]() �ֱ�
�ֱ�![]() �ڵ�
�ڵ�![]() ���̶���
���̶���![]() ��ʹ
��ʹ![]() �Ƶ�
�Ƶ�![]() ��ת����
��ת����![]() ______��
______��
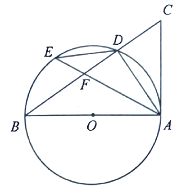
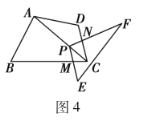
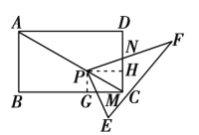
��3����չ̽������ͼ4�����ı���![]() ����������
����������![]() ��
��![]() ��ʱ����
��ʱ����![]() �ڶԽ���
�ڶԽ���![]() �ϣ�
�ϣ�![]() �ֱ�
�ֱ�![]() �ڵ�
�ڵ�![]() ���̶���
���̶���![]() ��ʹ
��ʹ![]() �Ƶ�
�Ƶ�![]() ��ת����̽��
��ת����̽��![]() ��ֵ����˵�����ɣ�
��ֵ����˵�����ɣ�
���𰸡���1����![]() ����
����![]() ����2��
����2��![]() ����3��
����3��![]() �����ɼ�����
�����ɼ�����
��������
��1�������ж���PMC�ס�ABC���ٸ������������εĶ�Ӧ�߳ɱ���������⣻�����â��еķ������������PMCN�ı߳���
��2���ȹ�P��PG��BC��G����PH��CD��H���ж���PGM�ס�PHN���ٸ������������ε������Լ�ƽ���߷��߶γɱ������������Ƶ����㼴�ɣ�
��3���ȹ�P��PG��AB����PH��AD�������������B+��D=180�����ж���PGM�ס�PHN���ٸ������������ε������Լ�ƽ���߷��߶γɱ������������Ƶ����㼴�ɣ�
��1����![]()
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
���ı���![]() �������Σ����ı���
�������Σ����ı���![]() �ı߳���
�ı߳���![]() ��
��
��![]()
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() �����ı���
�����ı���![]() �����Ϊ
�����Ϊ![]() ��
��
��2��![]()
��ͼ��
����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]()
![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��3��![]() ���������£�
���������£�

��ͼ������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��
��![]() ��
��![]() ��
��