题目内容
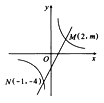
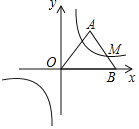
【题目】如图，等腰△OAB的底边OB恰好在x轴上，反比例函数y＝
的图象经过AB的中点M，若等腰△OAB的面积为24，则k＝（ ）
A. 24B. 18C. 12D. 9
【答案】B
【解析】
先连接OM，过A作AC⊥x轴于点C，过M作MD⊥x轴于点D，根据相似三角形的判定得到△BDM∽△BCA，则根据相似三角形的性质得到
＝（
）2＝
，再根据三角形的面积公式进行计算得到S△OMD＝9，因为反比例函数y＝
的图象经过点M，则S△OMD＝
k＝9，计算即可得到答案.
解：如图，连接OM，过A作AC⊥x轴于点C，过M作MD⊥x轴于点D，
则MD∥AC，
∴△BDM∽△BCA，
∴＝（）2＝，
∵OA＝AB，AC⊥OB，
∴OC＝CB，
∴S△BAC＝S△BAO＝×24＝12，
∴S△BMD＝S△BAC＝3．
∵M点是AB的中点，
∴S△OMB＝S△BAO＝12，
∴S△OMD＝S△OMB﹣S△BMD＝12﹣3＝9，
∵反比例函数y＝的图象经过点M，
∵S△OMD＝k＝9，
∴k＝18．
故选：B．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
