题目内容
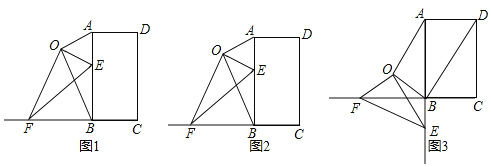
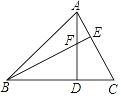
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)若∠ABD=45°,AC=3时,求BF的长.
【答案】(1)见解析;(2)3
【解析】
(1)根据双垂直得出∠DBF=∠DAC,然后根据直角得出三角形相似;(2)根据tan∠ABD=1,∠ADB=90°得出AD=BD,然后根据△ACD和△BFD相似得出BF=AC=3.
(1)∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∴△ACD∽△BFD.
(2)∵∠ABD=45°,∠ADB=90°
∴AD=BD,
∵△ACD∽△BFD,
∴![]() ,
,
∴BF=AC=3.

练习册系列答案
相关题目
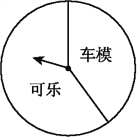
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?