题目内容
【题目】在平面直角坐标系中，抛物线
的最高点的纵坐标是2．
（1）求抛物线的表达式；
（2）将抛物线在
之间的部分记为图象
，将图象沿直线x=1翻折，翻折后图象记为
，图象和组成G，直线
:
和图象G在x轴上方的部分有两个公共点，求k的取值范围；
（3）直线:
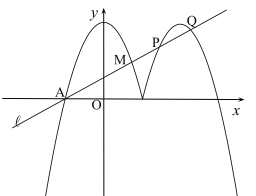
与图象G在x轴上方的部分分别交于A、M、P、Q四点，若AM=2PQ，求
的值．
【答案】（1）
；（2）k的取值范围为：
；（3）
．
【解析】
（1）根据抛物线顶点坐标公式，求出a的值，进而即可求解；
（2）分别求出当直线
与抛物线在x轴上方部分只有一个交点时，k的值，以及当直线与抛物线
在x轴上方部分只有一个交点时，k的值，即可得到k的取值范围；
（3）联立
，联立
，分别得到
，
，结合
，得到关于k的方程，即可求解．
（1）∵
，解得：a=-2，
∴抛物线的表达式为：；
（2）当直线与抛物线在x轴上方部分只有一个交点时，
联立，得：
，
∴
，即：
，解得：
，
∵
（舍去）
∴
，
将图像
沿直线x=1翻折，翻折后图像记为
：（
），
当直线与抛物线在x轴上方部分只有一个交点时，
联立，得：
，
∴
，解得：k=4，
∴k的取值范围：；
（3）联立，得：，
解得：
，
∴，
联立，得：，
同理得：，
∵，
∴
，
∴
=2
解得：或
∵
，
∴．
练习册系列答案
相关题目
