题目内容
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,AC=10,将BC向BA方向翻折过去,使点C落在BA上的点C′,折痕为BE,则EC的长度是 .
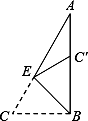

 .
.试题分析:作ED⊥BC于D,可得含30°的Rt△CED及含45°的直角三角形BED,设所求的EC为x,则CD=0.5x,BD=ED=
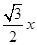 ,根据BC=5列式求值即可.
,根据BC=5列式求值即可.试题解析:作ED⊥BC于D,由折叠的性质可知∠DBE=∠ABE=45°,
设所求的EC为x,则CD=
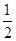 x,BD=ED=
x,BD=ED=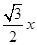 ,
,∵∠ABC=90°,∠C=60°,AC=10,
∴BC=AC×cosC=5,
∵CD+BD=5,
∴
 .
.考点: 翻折变换(折叠问题).

练习册系列答案
相关题目
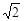 ≈1.414,
≈1.414,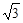 ≈1.732)
≈1.732)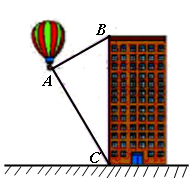
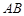 ,在
,在 处测得楼顶
处测得楼顶 的仰角为30°,向高楼前进100米到达
的仰角为30°,向高楼前进100米到达 处,在
处,在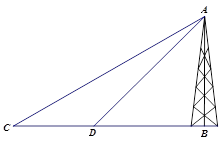
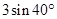
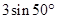
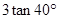
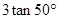
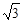 ,斜边AB的长为2
,斜边AB的长为2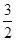 ,如果将△ABC沿直线l翻折后,点B落在边AC的中点处,直线l与边BC交于点D,那么BD的长为 .
,如果将△ABC沿直线l翻折后,点B落在边AC的中点处,直线l与边BC交于点D,那么BD的长为 .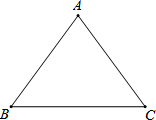

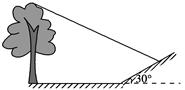
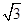 )米
)米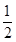 ,cosB=
,cosB=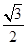 ,则△ABC的形状是
,则△ABC的形状是