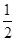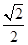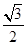题目内容
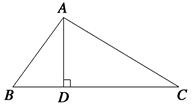
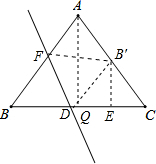
如图，在△ABC中，AB=AC，BC=8，tanC=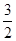
，如果将△ABC沿直线l翻折后，点B落在边AC的中点处，直线l与边BC交于点D，那么BD的长为 ．
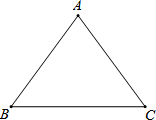
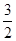，如果将△ABC沿直线l翻折后，点B落在边AC的中点处，直线l与边BC交于点D，那么BD的长为 ．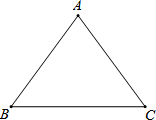
首先根据已知得出△ABC的高以及B′E的长，利用勾股定理求出BD即可．
解：过点A作AQ⊥BC于点Q，
∵AB=AC，BC=8，tanC=，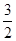
∴
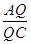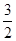=，QC=BQ=4，
∴AQ=6，
∵将△ABC沿直线l翻折后，点B落在边AC的中点处，
过B′点作B′E⊥BC于点E，
∴B′E=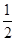
AQ=3，
∴
=
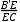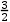， ∴EC=2，
设BD=x，则B′D=x，
∴DE=8﹣x﹣2=6﹣x，
∴x2=（6﹣x）2+32，
解得：x=，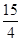
直线l与边BC交于点D，那么BD的长为：．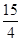
故答案为：．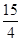
解：过点A作AQ⊥BC于点Q，
∵AB=AC，BC=8，tanC=
，∴
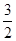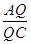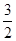=，QC=BQ=4，∴AQ=6，
∵将△ABC沿直线l翻折后，点B落在边AC的中点处，
过B′点作B′E⊥BC于点E，
∴B′E=
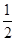AQ=3，∴
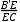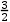=， ∴EC=2，设BD=x，则B′D=x，
∴DE=8﹣x﹣2=6﹣x，
∴x2=（6﹣x）2+32，
解得：x=
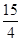，直线l与边BC交于点D，那么BD的长为：
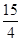．故答案为：
．
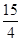练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
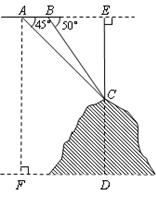
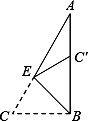
，则折痕DE长为 。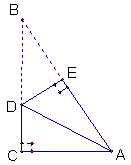
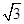，则此斜坡的坡角为 ．
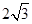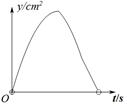
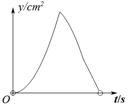
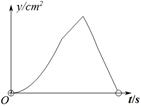
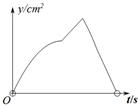
cm， E为CD边上的中点，点P从点A沿折线AE-EC运动到点C时停止，点Q从点A沿折线AB-BC运动到点C时停止，它们运动的速度都是1cm/s.如果点P，Q同时开始运动，设运动时间为t（s），△APQ的面积为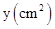
，则y与t的函数关系的图象可能是（ ）
AB的长为半径画弧，两弧相交于点M、N；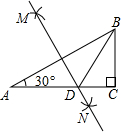
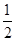，AC＝3，AB＝4，求BD的长．(结果保留根号)
