题目内容
【题目】如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此九(2)班数学兴趣小组对本班同学天饮用饮品的情况进行了调查,发现大致可分为四种:A非碳酸饮料,B瓶装矿泉水,C碳酸饮料,D白开水.
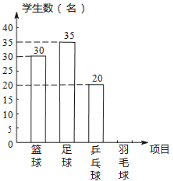
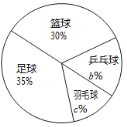
根据统计结果绘制如下两个统计图,根据统计图提供的信息解答下列问题:
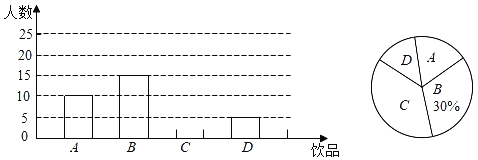
(1)九(2)班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如表),则该班同学每天用于饮品的人均花费是多少元?
饮品名称 | 白开水 | 瓶装矿泉水 | 碳酸饮料 | 非碳酸饮料 |
平均价格(元/瓶) | 0 | 2 | 3 | 4 |
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名同学(其中有两位班长记为a,b,其余三位记为c,d,e)中随机抽取2名作良好习惯监督员,请用列表法或画树状图的方法,求出抽到的2名同学都不是班长的概率.
【答案】(1)九(2)班级的学生人数为50(人);补全图形见解析;(2)该班同学每天用于饮品的人均花费是2.2元;(3)恰好抽到的2名同学都不是班长的概率![]()
【解析】
(1)由B种人数除以所占百分比即可得出这个班级总人数;求出选择C饮品的人数,补全条形统计图即可;
(2)由平均数定义即可得出答案;
(3)列表得到所有可能的结果数,由概率公式即可得出答案.
解:(1)九(2)班级的学生人数为15÷30%=50(人);
选择C饮品的人数为50﹣(10+15+5)=20(人),
补全条形统计图如下:
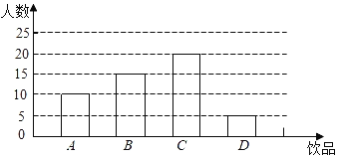
(2)该班同学每天用于饮品的人均花费=![]() =2.2(元),
=2.2(元),
答:该班同学每天用于饮品的人均花费是2.2元;
(3)列表如下:
a | b | c | d | e | |
a | ﹣﹣﹣ | (b,a) | (c,a) | (d,a) | (e,a) |
b | (a,b) | ﹣﹣﹣ | (c,b) | (d,b) | (e,b) |
c | (a,c) | (b,c) | ﹣﹣﹣ | (d,c) | (e,c) |
d | (a,d) | (b,d) | (c,d) | ﹣﹣﹣ | (e,d) |
e | (a,e) | (b,e) | (c,e) | (d,e) | ﹣﹣﹣ |
所有等可能的情况有20种,其中抽到的2名同学都不是班长的结果数为6种,
所以恰好抽到的2名同学都不是班长的概率=![]() =
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为增强公民的节约意识,合理利用天然气费源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调能后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出75m3的部分 | 2 |
超出75 m3不超过125 m3的部分 | a |
超出125 m2的部分 | a+0.5 |
(1)若某户3月份用气量为60 m3,则应交费多少元?
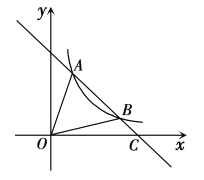
(2)调价后每月支付燃气费用y(元)与每月用气量x(m3)的函数关系如图所示,求a的值及线段AB对应的一次函数的表达式;
(3)求射线BC对应的一次函数的表达式.