��Ŀ����
����Ŀ����ͼ��һ�κ���![]() ��
��![]() ����ͼ���������ύ��A��B���㣬�뷴��������
����ͼ���������ύ��A��B���㣬�뷴��������![]() ��
��![]() ����ͼ����M��N���㣬����M��MC��y���ڵ�C����֪CM=1��
����ͼ����M��N���㣬����M��MC��y���ڵ�C����֪CM=1��
��1����![]() ��ֵ��
��ֵ��
��2����![]() �����������Ľ���ʽ��
�����������Ľ���ʽ��
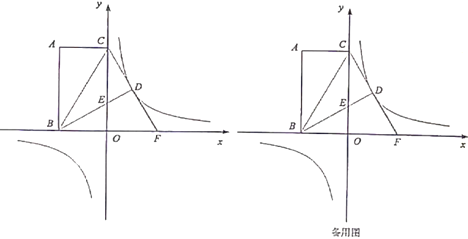
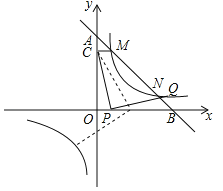
��3���ڣ�2���������£����P��x�ᣨ��ԭ��O�⣩��һ�㣬���߶�CP�Ƶ�P��˳ʱ�����ʱ����ת90��õ��߶�PQ������P����ʱ����Q�ܷ��ڷ�����������ͼ���ϣ�����ܣ�������еĵ�Q�����ꣻ������ܣ���˵�����ɣ�
���𰸡���1��5����2��![]() ����3����Q������Ϊ��2+
����3����Q��������2+![]() ����2+
����2+![]() ����2��
����2��![]() ����2��
����2��![]() ����2����2����
����2����2����
��������
��1�����ݵ�M��������뷴������ϵ��![]() �У��ɵý��ۣ�
�У��ɵý��ۣ�
��2�����ݡ�ACM�ס�ADN����![]() ����CM=1��DN=4��ͬ����N�����꣬���뷴��������ʽ�пɵ�k2��ֵ��
����CM=1��DN=4��ͬ����N�����꣬���뷴��������ʽ�пɵ�k2��ֵ��
��3����ͼ2����P��x�����������ʱ����P˳ʱ����ת����Q�����ݡ�COP�ա�PHQ����CO=PH��OP=QH����P��x��0������ʾQ��x+4��x�������뷴���������Ĺ�ϵʽ�пɵ�Q���������ꣻ
��ͼ3����P��x��ĸ�������ʱ��
��ͼ4����P��x�����������ʱ����P��ʱ����ת����Q��ͬ���ɵý��ۣ�
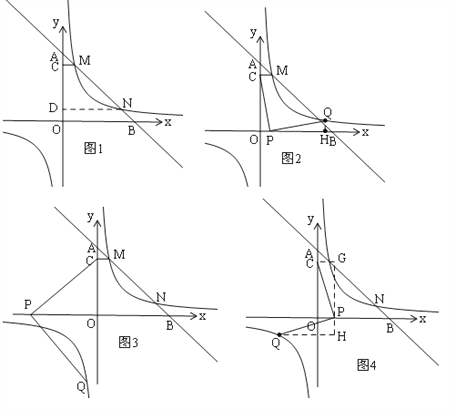
�⣺��1����ͼ1��
��MC��y���ڵ�C����CM=1��
��M�ĺ�����Ϊ1����x=1ʱ��y=k1+5��
��M��1��k1+5����
��M�ڷ�����������ͼ���ϣ�
��1����k1+5��=k2��
��k2��k1=5��
��2����ͼ1����N��ND��y����D��
��CM��DN��
���ACM�ס�ADN��
��![]() ��
��
��CM=1��
��DN=4����x=4ʱ��y=4k1+5��
��N��4��4k1+5����
��4��4k1+5��=k2�٣�
�ɣ�1���ã�k2��k1=5��
��k1=k2��5�ڣ�
�Ѣڴ���ٵã�4��4k2��20+5��=k2��k2=4��
�෴���������Ľ���ʽ��![]() ��
��
��3������P����ʱ����Q���ڷ�����������ͼ���ϣ�
��ͼ2��CP=PQ����CPQ=90�㣬��Q��QH��x����H��
�ã���COP�ա�PHQ��
��CO=PH��OP=QH��
�ɣ�2��֪�������������Ľ���ʽ��![]() ��
��
��x=1ʱ��y=4��
��M��1��4����
��OC=PH=4��
��P��x��0����
��Q��x+4��x����
����Q���ڷ�����������ͼ����ʱ��x��x+4��=4��x2+4x+4=8��x=��2��![]() ��
��
��x=��2+![]() ʱ��x+4=2+
ʱ��x+4=2+![]() ��
��
��ͼ2��Q��2+![]() ����2+
����2+![]() ����
����
��x=��2��![]() ʱ��x+4=2��
ʱ��x+4=2��![]() ����ͼ3��Q��2��
����ͼ3��Q��2��![]() ����2��
����2��![]() ����
����
��ͼ4��CP=PQ����CPQ=90�㣬
��P��x��0������P��GH��y�ᣬ��C��CG��GH����Q��QH��GH���ã���CPG�ա�PQH��
��PG=QH=4��CG=PH=x��
��Q��x��4����x����
ͬ���ã���x��x��4��=4����ã�x1=x2=2��
��Q����2����2����
������������Q��������2+![]() ����2+
����2+![]() ����2��
����2��![]() ����2��
����2��![]() ����2����2����
����2����2����

 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�