题目内容
【题目】一张直角三角形纸片ABC,∠ACB=90°,AB=10,AC=6,点D为BC边上的任一点,沿过点D的直线折叠,使直角顶点C落在斜边AB上的点E处,当△BDE是直角三角形时,则CD的长为________.
【答案】3或![]()
【解析】
分∠BDE=90°、∠BED=90°两种情况,证△BDE与△ABC相似,根据对应边成比例及折叠的性质即可求解.
∵∠ACB=90°,AB=10,AC=6,
∴BC=8
由折叠可得:CD=DE
设CD=DE=x
如图,当∠BDE=90°时
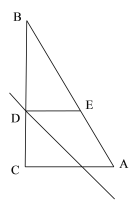
∵∠BDE=∠ACB=90°,∠B=∠B
∴△BDE∽△BCA
∴![]() 即
即![]()
解得:![]()
如图,当∠BED=90°时
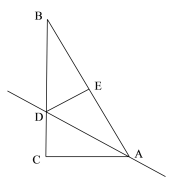
∵∠BED=∠ACB=90°,∠B=∠B
∴△BDE∽△BAC
∴![]() ,即
,即![]()
解得:x=3
故答案为:3或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目