题目内容
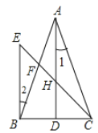
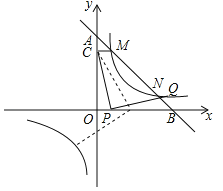
【题目】如图，在平面直角坐标系中，矩形
的顶点
在
轴上，
在
轴上，把矩形沿对角线
所在的直线对折，点
恰好落在反比例函数
的图象上点
处，
与轴交于点
，延长
交轴于点
，点刚好是
的中点.已知的坐标为
．
（1）求反比例函数的函数表达式；
（2）若
是反比例函数图象上的一点，
点在轴上，若以
为顶点的四边形是平行四边形，请直接写出点的坐标_________.
【答案】（1）
；（2）
，
，（
，0）．
【解析】
(1)证得BD是CF的垂直平分线，求得
，作DG⊥BF于G，求得点D的坐标为
，从而求得反比例函数的解析式；
(2)分3种情形，分别画出图形即可解决问题．
(1) ∵四边形ABOC是矩形，
∴AB=OC，AC=OB，
，
根据对折的性质知，
，
∴
，
，AB=DB，
又∵D是CF的中点，
∴BD是CF的垂直平分线，
∴BC=BF，
，
∴
，
∵
，
∴，
∵点B的坐标为
，
∴
，
在
中，
，
，
，
∴
，
过D作DG⊥BF于G，如图，
在
中，
，
，
，
∴
，
，
∴
，
∴点D的坐标为 ，
代入反比例函数的解析式
得：
，
∴反比例函数的解析式
；
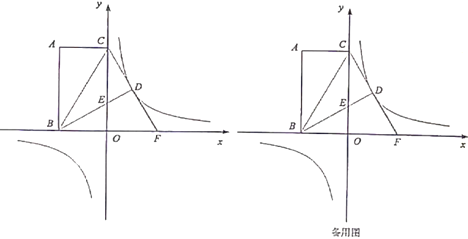
(2) 如图①、②中，作EQ∥x轴交反比例函数的图象于点Q，
在
中， 
，
，
∴
，
∴点E的坐标为
，
点Q纵坐标与点E纵坐标都是
，代入反比例函数的解析式得：
，
解得：
，
∴点Q的坐标为
，
∴
，
∵
四点构成平行四边形，
∴
∴点
的坐标分别为
，
；
如图③中，
构成平行四边形，作QM∥y轴交
轴于点M，
∵四边形为平行四边形，
∴
，
，
∴
，
∴
，
，
∴点
的坐标为
，
∴
∴
，
∴点
的坐标为
，
综上，符合条件点
的坐标有：
，
，；
练习册系列答案
名校课堂系列答案
相关题目
