题目内容
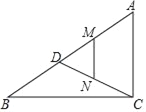
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.

【答案】(1)证明见解析;(2)30°.
【解析】
由三角形的内角和可求出∠ECB=35°,根据角平分线的定义可求∠ACB=70°,进而可求出∠BAC=70°,从而结论可证;
(2)由AP是△AEC边EC上的中线可知AP=PC,从而∠PAC=∠PCA,由CE是∠ACB的平分线,可证∠PAC=∠PCA=∠PCD,从而可求出∠PAC的度数,然后求出∠BAD=60°,继而可求出∠B的值.
(1)证明:∵∠B=40°,∠AEC=75°,
∴∠ECB=∠AEC﹣∠B=35°,
∵CE平分∠ACB,
∴∠ACB=2∠BCE=70°,
∠BAC=180°﹣∠B﹣∠ACB=180°﹣40°﹣70°=70°,
∴∠BAC=∠BCA,
∴AB=AC.
(2)∵∠BAC=90°,AP是△AEC边EC上的中线,
∴AP=PC,
∴∠PAC=∠PCA,
∵CE是∠ACB的平分线,
∴∠PAC=∠PCA=∠PCD,
∵∠ADC=90°,
∴∠PAC=∠PCA=∠PCD=90°÷3=30°,
∴∠BAD=60°,
∵∠ADB=90°,
∴∠B=90°﹣60°=30°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目