Question

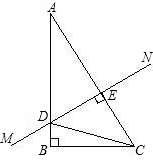
菱形ABCD中，AE垂直平分BC，垂足为E，AB=4cm．那么，菱形ABCD的面积是______cm²，对角线BD的长是______cm．

Answer 1

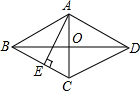
∵四边形ABCD是菱形，
∴AB=BC=4cm，又∵AE垂直平分BC，
∴BE=EC=

1

2

×BC=

1

2

×4=2cm
在Rt△ABE中，AB=4cm，BE=2cm
由勾股定理得AE=

AB2-BE2

=

42-22

=2

3

∴S_菱形ABCD=BC•AE=4×2

3

=8

3

cm²∵AB=BC=4cm，
在Rt△AEC中，AE=2

3

cm，EC=2cm
∴AC=

(2 3 )2+22

=4，OC=

1

2

AC=2
在Rt△BCO中，BC=4cm，OC=2cm，
∴OB=

BC2-OC2

=

42-22

=2

3

对角线BD的长=2•OB=2×2

3

=4

3

cm．
菱形ABCD的面积是8

3

cm²，对角线BD的长是4

3

cm．