题目内容
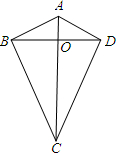
两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有______.(填序号).
①AC⊥BD;②AC、BD互相平分;③AC平分∠BCD;④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为
AC•BD.
①AC⊥BD;②AC、BD互相平分;③AC平分∠BCD;④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为
| 1 |
| 2 |

∵在△ABC与△ADC中,
,
∴△ABC≌△ADC(SSS).
∴∠BAO=∠DAO,∠BCO=∠DCO,即AC平分∠BCD.故③正确;
∵AC平分∠BAD、∠BCD,△ABD与△BCD均为等腰三角形,
∴AC、BD互相垂直,但不平分.故①正确,②错误;
当AC2≠AB2+BC2时,∠ABC≠90°.同理∠ADC≠90°.故④错误;
∵AC、BD互相垂直,
∴筝形ABCD的面积为:
AC•BO+
AC•OD=
AC•BD.
故⑤正确;
综上所述,正确的说法是①③⑤.
故答案是:①③⑤.
|
∴△ABC≌△ADC(SSS).
∴∠BAO=∠DAO,∠BCO=∠DCO,即AC平分∠BCD.故③正确;
∵AC平分∠BAD、∠BCD,△ABD与△BCD均为等腰三角形,
∴AC、BD互相垂直,但不平分.故①正确,②错误;
当AC2≠AB2+BC2时,∠ABC≠90°.同理∠ADC≠90°.故④错误;
∵AC、BD互相垂直,
∴筝形ABCD的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故⑤正确;
综上所述,正确的说法是①③⑤.
故答案是:①③⑤.

练习册系列答案
相关题目