题目内容
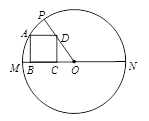
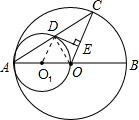
如图:AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于D,DE⊥OC,垂足为E.
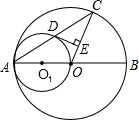
(1)求证:AD=DC;
(2)求证:DE是⊙O1的切线;
(3)如果OE=EC,请判断四边形O1OED是什么四边形,并证明你的结论.

(1)求证:AD=DC;
(2)求证:DE是⊙O1的切线;
(3)如果OE=EC,请判断四边形O1OED是什么四边形,并证明你的结论.
(1)证明见试题解析;(2)证明见试题解析;(3)正方形,证明见试题解析.
试题分析:(1)连OD可得OD⊥AC,又有OA=OC,所以第一问可求解;
(2)证明O1D⊥DE即可;
(3)如果OE=EC,又D为AC的中点,所以四条边相等,再根据角之间的关系,即可得出其形状.
试题解析:(1)连接OD,∵AO为圆O1的直径,则∠ADO=90°.∵AC为⊙O的弦,OD为弦心距,∴AD=DC.
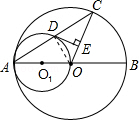
(2)∵D为AC的中点,O1为AO的中点,∴O1D∥OC.又DE⊥OC,∴DE⊥O1D,∴DE与⊙O1相切;
(3)如果OE=EC,又D为AC的中点,∴DE∥O1O,又O1D∥OE,∴四边形O1OED为平行四边形.又∠DEO=90°,O1O=O1D,∴四边形O1OED为正方形.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 中,将一块含
中,将一块含 的直角三角板的
的直角三角板的 两点(点
两点(点 在
在 内部),
内部), 与
与 交于点
交于点 ,
, 交于点
交于点 .
.
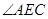 的度数;
的度数; 的中点,求
的中点,求 的值;
的值;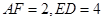 ,求
,求 的长.
的长.
 把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.
把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式. =6cm,
=6cm, 是
是 ,连接
,连接 .
.
 30°,求PC的长;
30°,求PC的长; 的平分线交
的平分线交 ,你认为∠
,你认为∠ 的大小是否发生变化?若变化,请说明理由;若不变,求出∠
的大小是否发生变化?若变化,请说明理由;若不变,求出∠