题目内容
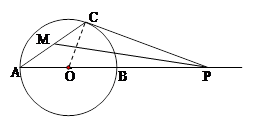
如图,⊙O的直径 =6cm,
=6cm, 是
是 延长线上的一点,过
延长线上的一点,过 点作⊙O的切线,切点为
点作⊙O的切线,切点为 ,连接
,连接 .
.

(1)若 30°,求PC的长;
30°,求PC的长;
(2)若点 在
在 的延长线上运动,
的延长线上运动, 的平分线交
的平分线交 于点
于点 ,你认为∠
,你认为∠ 的大小是否发生变化?若变化,请说明理由;若不变,求出∠
的大小是否发生变化?若变化,请说明理由;若不变,求出∠ 的值.
的值.
 =6cm,
=6cm, 是
是 延长线上的一点,过
延长线上的一点,过 点作⊙O的切线,切点为
点作⊙O的切线,切点为 ,连接
,连接 .
.
(1)若
 30°,求PC的长;
30°,求PC的长;(2)若点
 在
在 的延长线上运动,
的延长线上运动, 的平分线交
的平分线交 于点
于点 ,你认为∠
,你认为∠ 的大小是否发生变化?若变化,请说明理由;若不变,求出∠
的大小是否发生变化?若变化,请说明理由;若不变,求出∠ 的值.
的值.(1)PC=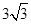 ;(2)∠CMP=45°,即∠CMP的大小不发生变化.
;(2)∠CMP=45°,即∠CMP的大小不发生变化.
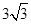 ;(2)∠CMP=45°,即∠CMP的大小不发生变化.
;(2)∠CMP=45°,即∠CMP的大小不发生变化.试题分析:(1)在圆中线段利用由切线定理求得∠OCP=90°,进而利用直角三角形PCO中的线段,结合解直角三角形求得PC即可.
(2)先根据切线的性质得到∠OCP=90°,再利用角平分线和圆周角的性质得到2∠A+2∠APM=90,即∠A+∠APM=45°,利用三角形的外角等于不相邻的两个内角和可知∠CMP=∠A+∠APM=45°,所以∠CMP的大小不发生变化.
试题解析:
解:(1)连接
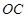 ,
,PC是⊙O的切线,
∴∠OCP=90°.
∵
 30°,OC=
30°,OC=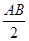 =3,
=3,∴
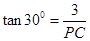 ,即PC=
,即PC=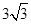 .
. (2)∠CMP的大小不发生变化.
∵PM是∠CPA的平分线,
∴∠CPM=∠MPA.
∵OA=OC,∴∠A=∠ACO.
在△APC中,
∵∠A+∠ACP+∠CPA=180°,
∴2∠A+2∠MPA=90°,∠A+∠MPA=45°.
∴∠CMP=∠A+∠MPA=45°.即∠CMP的大小不发生变化.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目
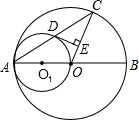







 圆周的一个扇形,将留下的扇形(阴影部分)围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )
圆周的一个扇形,将留下的扇形(阴影部分)围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )
 cm
cm cm
cm