题目内容
【题目】如图,已知抛物线经过点![]() ,
,![]() ,
,![]() .
.
![]() 求抛物线的函数表达式;
求抛物线的函数表达式;
![]() 求抛物线的顶点坐标;
求抛物线的顶点坐标;
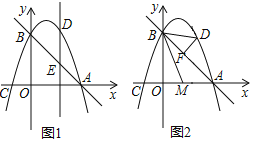
![]() 如图1,点D是抛物线上一动点,过D作y轴的平行线DE交直线AB于点E,当线段
如图1,点D是抛物线上一动点,过D作y轴的平行线DE交直线AB于点E,当线段![]() 时,请直接写出D点的横坐标;
时,请直接写出D点的横坐标;
![]() 如图2,当D为直线AB上方抛物线上一动点时,
如图2,当D为直线AB上方抛物线上一动点时,![]() 于F,设AC的中点为M,连接BD,BM,是否存在点D,使得
于F,设AC的中点为M,连接BD,BM,是否存在点D,使得![]() 中有一个角与
中有一个角与![]() 相等?若存在,请直接写出点D的横坐标;若不存在,请说明理由.
相等?若存在,请直接写出点D的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 点的横坐标为
点的横坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;(4)存在,D点的横坐标为
;(4)存在,D点的横坐标为![]() 或
或![]() .
.
【解析】
![]() 设交点式
设交点式![]() ,然后把B点坐标代入求出a得到抛物线解析式,然后把解析式
,然后把B点坐标代入求出a得到抛物线解析式,然后把解析式
![]() 把一般式化为顶点式得到抛物线的顶点坐标;
把一般式化为顶点式得到抛物线的顶点坐标;
![]() 易得直线AB的解析式为
易得直线AB的解析式为![]() ,设
,设![]() ,则
,则![]() ,利用题意得到
,利用题意得到![]() ,然后
,然后![]() 解绝对值方程即可;
解绝对值方程即可;
![]() 若
若![]() ,则
,则![]() ,作
,作![]() 轴于B,作
轴于B,作![]() 于H,
于H,![]() 于G,如图,证明
于G,如图,证明![]() ,再计算出
,再计算出![]() ,则
,则![]() ,设
,设![]() ,所以
,所以![]() ,然后解t的方程得到此时D点的横坐标
,然后解t的方程得到此时D点的横坐标![]() 若
若![]() ,作
,作![]() 轴于抛物线交于另一点
轴于抛物线交于另一点![]() ,作
,作![]() 轴交BD于G,如图3,则
轴交BD于G,如图3,则![]() ,
,![]() ,同理得
,同理得![]() ,则
,则![]() ,所以
,所以![]() ,接着求出直线BG的解析式为
,接着求出直线BG的解析式为![]() ,然后解方程组
,然后解方程组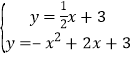 得D点坐标.
得D点坐标.
解:![]() 设抛物线解析式为
设抛物线解析式为![]() ,
,
把![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ,即
,即![]() ;
;
![]() ,
,
![]() 抛物线的顶点坐标为
抛物线的顶点坐标为![]() ;
;
![]() 易得直线AB的解析式为
易得直线AB的解析式为![]() ,
,
设![]() ,则
,则![]()
![]()
![]() ,
,
解方程![]() 得
得![]() ,
,![]() ;
;
解方程![]() 得
得![]() ,
,![]() ,
,
![]() 点的横坐标为
点的横坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;
;
![]() 存在.
存在.
抛物线的对称轴为直线![]() ,则
,则![]() ,
,
若![]() ,则
,则![]() ,
,
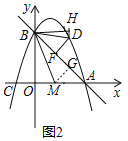
作![]() 轴于B,作
轴于B,作![]() 于H,
于H,![]() 于G,如图2,
于G,如图2,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
设![]() ,
,
![]()
整理得![]() ,解得
,解得![]() 舍去
舍去![]() ,
,![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,
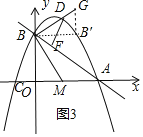
若![]() ,作
,作![]() 轴于抛物线交于另一点
轴于抛物线交于另一点![]() ,作
,作![]() 轴交BD于G,如图3,则
轴交BD于G,如图3,则![]() ,
,![]() ,
,
同理得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
易得直线BG的解析式为![]() ,
,
解方程组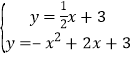 得
得![]() 或
或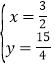 ,
,
![]() 点坐标为
点坐标为![]() ,
,
综上所述,D点的横坐标为![]() 或
或![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?