Question

【题目】如图，在△ABC中，已知AB＝AC＝4 cm，BC＝6 cm，D是BC的中点，以点D为圆心作一个半径为3 cm的圆，则下列说法正确的是(　　)

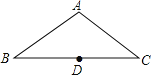
A. 点A在⊙D外 B. 点B在⊙D内 C. 点C在⊙D上 D. 无法确定

Answer 1

【答案】C

【解析】

要确定点与圆的位置关系，主要确定点与圆心的距离与半径的大小关系，设点与圆心的距离d，则d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．

连接AD，由等腰三角形三线合一得AD⊥BC，求出BD，根据勾股定理求出AD，和半径比较即可．

连接AD，

∵AB=AC=4cm，BC=6cm，D是BC的中点，

∴BD=CD=3cm，AD⊥BC，

∴∠ADB=90，

∴在Rt△ADB中，由勾股定理得：

AD= ==

∵<3，

∴点A在⊙D内，点C在⊙D上.

故选C.