题目内容
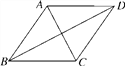
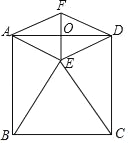
【题目】如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE.
(1)请直接写出∠AEB的度数,∠AEB= ;
(2)将△AED沿直线AD向上翻折,得△AFD.求证:四边形AEDF是菱形;
(3)连接EF,交AD于点 O,试求EF的长?
【答案】(1)75°;(2)证明见解析;(3)![]()
【解析】
试题(1)由正方形和等边三角形的性质得出∠ABE=30°,AB=BE,由等腰三角形的性质和三角形内角和定理即可求出∠AEB的度数;
(2)先判断出△ABE≌△DCE,得到AE=ED,再由翻折的性质即可得出结论;
(3)先由等边三角形的性质求出EH,进而得出OE,借助(2)的结论即可求出EF.
试题解析:(1)∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,AB=BC=CD,
∵△EBC是等边三角形,
∴BE=BC,∠EBC=60°,
∴∠ABE=90°-60°=30°,AB=BE,
∴∠AEB=∠BAE=![]() (180°-30°)=75°;
(180°-30°)=75°;
(2)∵四边形ABCD为正方形,
∴∠ABC=∠BCD=90°,AB=CD,
∵△BCE为等边三角形,
∴∠BCE=∠EBC=60°,BE=EC,
∴∠ABE=∠DCE=90°-60°=30°,
∴△ABE≌△DCE,
∴AE=ED,
∵△AED沿着AD翻折为△AFD,
∴AE=ED=AF=FD,
∴四边形AEDF是菱形;
(3)如图,
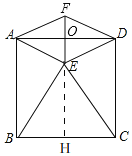
由翻折知,AE=AF,∠FAO=∠EAO,
∴EF⊥AD,过点E作EH⊥BC于H,
在等边三角形BCE中,BC=2,
∴EH=![]() BC=
BC=![]() ,
,
∴EO=OH-EH=AB-EH=2-![]() ,
,
∴EF=2EO=2(2-![]() )=4-2
)=4-2![]() .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目