题目内容
有编号1~30的30枚硬币正面朝上放在桌子上,先将编号为3的倍数的硬币翻个身,再将编号为4的倍数的硬币翻个身,最后仍有 个硬币正面朝上.
考点:数的整除特征,容斥原理
专题:数的整除
分析:第一次翻动时,所有编号为3的倍数的硬币被翻成正面朝下,共有30÷3=10个;第二次翻动时,所有编号为4的倍数的硬币被翻了一次,共有30÷4=7…2;但是两次翻动使得3和4的公倍数,被翻动了两次,状态恢复到最初,这样的数有30÷12=2…6;所以最后正面朝下的有10+7-2×2=13个.进而求出正面朝上的硬币的个数.
解答:
解:第一次翻动时,所有编号为3的倍数的硬币被翻成正面朝下,共有30÷3=10个;
第二次翻动时,所有编号为4的倍数的硬币被翻了一次,共有30÷4=7…2;
但是两次翻动使得3和4的公倍数,被翻动了两次,状态恢复到最初,这样的数有30÷12=2…6;
所以最后正面朝下的有10+7-2×2=13(个);
所以:正面朝上的就是30-13=17(个);
故答案为:17.
第二次翻动时,所有编号为4的倍数的硬币被翻了一次,共有30÷4=7…2;
但是两次翻动使得3和4的公倍数,被翻动了两次,状态恢复到最初,这样的数有30÷12=2…6;
所以最后正面朝下的有10+7-2×2=13(个);
所以:正面朝上的就是30-13=17(个);
故答案为:17.
点评:明确两次翻动使得3和4的公倍数,被翻动了两次,状态恢复到最初,这样的数有2个,是解答此题的关键.

练习册系列答案
相关题目
从装满100克20%的盐水中倒出50克盐水后,在用清水将杯加满,搅拌后再倒出50克盐水,然后再用清水将杯加满.如此反复三次,杯中盐水的浓度是( )
| A、2% | B、2.5% |
| C、3% | D、3.5% |
 如图,有两个可旋转标有从0到5的刻度盘.现在,两个刻度盘都在0的位置.同时掷大小两个骰子,按照下面的顺序旋转刻度盘.
如图,有两个可旋转标有从0到5的刻度盘.现在,两个刻度盘都在0的位置.同时掷大小两个骰子,按照下面的顺序旋转刻度盘. 一只兔子沿着方格的边从A到B,规定上只能往上或往右走,但是必须经过一座独木桥MN,这只兔子有
一只兔子沿着方格的边从A到B,规定上只能往上或往右走,但是必须经过一座独木桥MN,这只兔子有
 变为数字
变为数字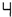 ,我们必须改变3个发光体,即F、C这二个发光体由亮变暗,E这个发光体由暗变亮.
,我们必须改变3个发光体,即F、C这二个发光体由亮变暗,E这个发光体由暗变亮.
