题目内容
如果三个连续正整数,中间一个是平方数,将这样的三个连续正整数的积叫做睿达数,那么所有小于2013的睿达数的最大公因数.
考点:完全平方数性质
专题:整除性问题
分析:根据题意可分析连续3个正整数里面必有一个数能被3、4和5整除,所以所得到的“睿达数”中必含有约数3、4和5,再将所有的公约数相乘就可求出最大公约数.
解答:
解:①任何三个连续正整数,必有一个能被3整除.所以,任何“睿达数”必有因数3.
②若三个连续正整数中间的数是偶数,它又是完全平方数,必定能为4整除;若中间的数是奇数,则第一和第三个数是偶数,所以任何“睿达数”必有因数4.
③完全平方数的个位只能是1、4、5、6、9和0,若其个位是5和0,则中间的数必能被5整除,若其个位是1和6,则第一个数必能被5整除,若其个位是4和9,则第三个数必能被5整除.所以,任何“睿达数”必有因数5.
④上述说明“睿达数”都有因数3、4、和5,也就有因数60,即所有的美妙数的最大公约数至少是60.
另一方面,60=3×4×5,60也是一个“睿达数”,美妙数的最大公约至多是60.
答:所有小于2013的睿达数的最大公约数只能是60.
②若三个连续正整数中间的数是偶数,它又是完全平方数,必定能为4整除;若中间的数是奇数,则第一和第三个数是偶数,所以任何“睿达数”必有因数4.
③完全平方数的个位只能是1、4、5、6、9和0,若其个位是5和0,则中间的数必能被5整除,若其个位是1和6,则第一个数必能被5整除,若其个位是4和9,则第三个数必能被5整除.所以,任何“睿达数”必有因数5.
④上述说明“睿达数”都有因数3、4、和5,也就有因数60,即所有的美妙数的最大公约数至少是60.
另一方面,60=3×4×5,60也是一个“睿达数”,美妙数的最大公约至多是60.
答:所有小于2013的睿达数的最大公约数只能是60.
点评:本题通过分析,找出美妙数的特点,从而找出最小的美妙数,再根据最大公因数的特点求解.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
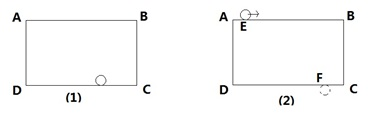
 如图,四边形ABCD是一个边长为100米的正方形,甲、乙两人同时从A点出发,甲沿逆时针方向每分钟行75米,乙沿顺时针方向每分钟行45米.请问:两人第一次在CD边(不包括C、D两点)上相遇,是出发以后的第几次相遇?
如图,四边形ABCD是一个边长为100米的正方形,甲、乙两人同时从A点出发,甲沿逆时针方向每分钟行75米,乙沿顺时针方向每分钟行45米.请问:两人第一次在CD边(不包括C、D两点)上相遇,是出发以后的第几次相遇?