题目内容
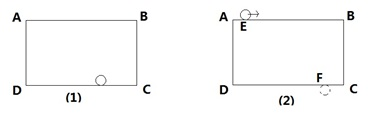
如图,长方形ABCD的长AB=14cm,宽BC=10cm,如图(1),一个半径为1cm的圆沿着长方形的四边内侧滚动一周,求圆滚过的面积;如图(2),E、F分别为AB、CD的点,且AE=
AB,FC:DF=2:5,一个半径为1cm的圆在长方形外侧连续地从E经过点B、C滚动到点F,求圆滚过的面积.(结果保留π)
| 1 |
| 7 |

考点:圆与组合图形
专题:竞赛专题
分析:(1)如图所示,圆滚过的面积=大长方形的面积-中间白色长方形的面积-四个直角处的面积和;四个直角处的面积和=边长为2厘米的正方形的面积-半径为1的圆的面积;据此解答即可.
(2)如图把圆滚过的面积分为7部分,3个长方形,起点、终点分别为两个半圆,两个角处分别为半径为2厘米的
圆;起点、终点加起来正好是一个半径长为1厘米圆的面积;两个角(两条红线之间)面积之和是半径为2厘米的半圆的面积;据此解答即可.

(2)如图把圆滚过的面积分为7部分,3个长方形,起点、终点分别为两个半圆,两个角处分别为半径为2厘米的
| 1 |
| 4 |

解答:
解:(1)中间空白长方形的长是14-4=10(厘米),宽是10-4=6(厘米);
14×10-10×6-(2×2-π×12)
=140-60-(4-π)
=80-4+π
=76+π(平方厘米)
答:圆滚过的面积是(76+π)平方厘米.
(2)AE=
AB=
×14=2(厘米),BE=14-2=12(厘米);
FC:DF=2:5,FC=
CD=
×14=4(厘米);
12×2+10×2+4×2+π×12+
×π×22
=24+20+8+π+2π
=52+3π(平方厘米)
答:圆滚过的面积是(52+3π)平方厘米.
14×10-10×6-(2×2-π×12)
=140-60-(4-π)
=80-4+π
=76+π(平方厘米)
答:圆滚过的面积是(76+π)平方厘米.
(2)AE=
| 1 |
| 7 |
| 1 |
| 7 |
FC:DF=2:5,FC=
| 2 |
| 2+5 |
| 2 |
| 7 |
12×2+10×2+4×2+π×12+
| 1 |
| 2 |
=24+20+8+π+2π
=52+3π(平方厘米)
答:圆滚过的面积是(52+3π)平方厘米.
点评:此题关键是作辅助线,将图形进行有效的分割,注意圆在角的顶点处的面积.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
长方体的长、宽、高都增加2倍体积( )
| A、增加2倍 | B、增加4倍 |
| C、增加26倍 | D、增加8倍 |