题目内容
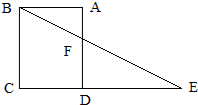
 如图,△DEF的面积是6平方厘米,AF=FB,BD=DE=EC,求△ABC的面积.
如图,△DEF的面积是6平方厘米,AF=FB,BD=DE=EC,求△ABC的面积.分析:连接AE,因为BD=DE,根据高一定时,三角形的面积与底成正比例的性质可得,三角形BEF的面积:三角形DEF的面积=2:1;所以三角形BEF的面积=12平方厘米,同理可得出三角形ABE的面积:三角形BEF的面积=2:1,所以三角形ABE的面积=24平方厘米;三角形ABC的面积:三角形ABE的面积=3:2,所以三角形ABC的面积=24×3÷2=36平方厘米.


解答:解:连接AE,因为AF=FB,BD=DE=EC,根据高一定时,三角形的面积与底成正比例的性质可得:
三角形BEF的面积:三角形DEF的面积=2:1;
所以三角形BEF的面积=6×2=12(平方厘米),
三角形ABE的面积:三角形BEF的面积=2:1,
所以三角形ABE的面积=12×2=24(平方厘米);
三角形ABC的面积:三角形ABE的面积=3:2,
所以三角形ABC的面积=24×3÷2=36(平方厘米),
答:三角形ABC的面积是36平方厘米.
三角形BEF的面积:三角形DEF的面积=2:1;
所以三角形BEF的面积=6×2=12(平方厘米),
三角形ABE的面积:三角形BEF的面积=2:1,
所以三角形ABE的面积=12×2=24(平方厘米);
三角形ABC的面积:三角形ABE的面积=3:2,
所以三角形ABC的面积=24×3÷2=36(平方厘米),
答:三角形ABC的面积是36平方厘米.
点评:此题主要考查了高一定时,三角形的面积与底成正比的关系的灵活应用.

练习册系列答案
相关题目
 如图,BD、CF将长方形ABCD分成4块,△DEF的面积是4cm2,△CED的面积是6cm2,则四边形ABEF的面积是
如图,BD、CF将长方形ABCD分成4块,△DEF的面积是4cm2,△CED的面积是6cm2,则四边形ABEF的面积是 如图长方形ABCD的面积是36平方厘米,且
如图长方形ABCD的面积是36平方厘米,且 如图,平行四边形ABCD的面积为40平方厘米,E是CD边延长线上的一点,BE与AD交于点F.已知三角形ABF的面积比三角形DEF的面积大7平方厘米,且CD=6厘米,那么DE的长度是
如图,平行四边形ABCD的面积为40平方厘米,E是CD边延长线上的一点,BE与AD交于点F.已知三角形ABF的面积比三角形DEF的面积大7平方厘米,且CD=6厘米,那么DE的长度是