题目内容
 如图长方形ABCD的面积是36平方厘米,且
如图长方形ABCD的面积是36平方厘米,且| AE |
| ED |
| CF |
| FD |
| 1 |
| 2 |
分析:连接EC,则三角形ABE和三角形ECD的面积和等于长方形的面积的一半,即36×
=18平方厘米,又因三角形ABE和三角形ECD底边AE和ED上的高相等,DE=2AE,所以三角形ABE的面积就等于三角形ABE和三角形ECD的面积和的
,即18×
=6平方厘米,三角形EDC的面积就等于18×
=12平方厘米,同理可得:三角形DEF的面积等于三角形EDC的面积的
,据此即可得解.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:三角形ABE和三角形ECD的面积和等于长方形的面积的一半,即36×
=18(平方厘米),
又因三角形ABE和三角形ECD底边AE和ED上的高相等,DE=2AE,
所以三角形ABE的面积就等于三角形ABE和三角形ECD的面积和的
,
即18×
=6(平方厘米),
三角形EDC的面积就等于18×
=12(平方厘米),
同理可得:三角形DEF的面积等于三角形EDC的面积的
,
即12×
=8(平方厘米),
答:三角形ABE的面积是6平方厘米,三角形DEF的面积是8平方厘米.
| 1 |
| 2 |
又因三角形ABE和三角形ECD底边AE和ED上的高相等,DE=2AE,
所以三角形ABE的面积就等于三角形ABE和三角形ECD的面积和的
| 1 |
| 3 |
即18×
| 1 |
| 3 |
三角形EDC的面积就等于18×
| 2 |
| 3 |
同理可得:三角形DEF的面积等于三角形EDC的面积的
| 2 |
| 3 |
即12×
| 2 |
| 3 |
答:三角形ABE的面积是6平方厘米,三角形DEF的面积是8平方厘米.
点评:解答此题的主要依据是:等高不等底的面积比等于其对应底的比,三角形的面积是与其等底等高的平行四边形面积的一半.

练习册系列答案
相关题目
 如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE是
如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE是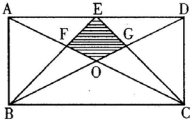 如图长方形ABCD的边AD=8cm,AB=6cm,E为AD中点,对角线AC、BD交于O点.BE、CE交两对角线分别交于F、G点,△ABF的面积为7.5cm2,求阴影部分EFOG的面积.
如图长方形ABCD的边AD=8cm,AB=6cm,E为AD中点,对角线AC、BD交于O点.BE、CE交两对角线分别交于F、G点,△ABF的面积为7.5cm2,求阴影部分EFOG的面积. 如图长方形ABCD的长AB=36厘米,宽BC=24厘米,三角形甲和三角形乙的面积各占长方形面积的
如图长方形ABCD的长AB=36厘米,宽BC=24厘米,三角形甲和三角形乙的面积各占长方形面积的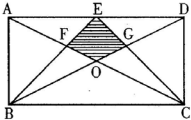 如图长方形ABCD的边AD=8cm,AB=6cm,E为AD中点,对角线AC、BD交于O点.BE、CE交两对角线分别交于F、G点,△ABF的面积为7.5cm2,求阴影部分EFOG的面积.
如图长方形ABCD的边AD=8cm,AB=6cm,E为AD中点,对角线AC、BD交于O点.BE、CE交两对角线分别交于F、G点,△ABF的面积为7.5cm2,求阴影部分EFOG的面积.