题目内容
 如图,BD、CF将长方形ABCD分成4块,△DEF的面积是4cm2,△CED的面积是6cm2,则四边形ABEF的面积是
如图,BD、CF将长方形ABCD分成4块,△DEF的面积是4cm2,△CED的面积是6cm2,则四边形ABEF的面积是11
11
平方厘米.分析:由题意可知:三角形FDE和三角形DEC等高不等底,则其面积比就等于对应底的比,即FE:EC=4:6=2:3,同理DE:EB=2:3,则三角形DEC的面积与三角形EBC的面积比也是2:3,三角形DEC的面积已知于是可以求出三角形EBC的面积,又因三角形DEC与三角形EBC的面积和是长方形的面积的一半,从而可以求出上半场ABEF的面积.
解答:解:因为S△FDES:△DEC=4:6=2:3,
则S△DEC:S△EBC=2:3,
即S△EBC=6×
=9(平方厘米),
所以S△DBC=
S长方形ABCD=6+9=15(平方厘米),
则S四边形ABEF=15-4=11(平方厘米);
答:四边形ABEF的面积是11平方厘米.
故答案为:11.
则S△DEC:S△EBC=2:3,
即S△EBC=6×
| 3 |
| 2 |
所以S△DBC=
| 1 |
| 2 |
则S四边形ABEF=15-4=11(平方厘米);
答:四边形ABEF的面积是11平方厘米.
故答案为:11.
点评:解答此题的主要依据是:等高不等底的三角形的面积比,就等于其对应底的比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012?郑州模拟)将自然数1~100排列如图:
(2012?郑州模拟)将自然数1~100排列如图: 如图:BD、CF将长方形ABCD分成四块,红色三角形面积是4平方厘米,黄色三角形面积是6平方厘米,问绿色四边形面积是多少平方厘米?
如图:BD、CF将长方形ABCD分成四块,红色三角形面积是4平方厘米,黄色三角形面积是6平方厘米,问绿色四边形面积是多少平方厘米? 如图BD、CF将长方形分成四块,△DEF面积是6平方厘米,△CDE面积是8平方厘米,那么四边形ABEF的面积是
如图BD、CF将长方形分成四块,△DEF面积是6平方厘米,△CDE面积是8平方厘米,那么四边形ABEF的面积是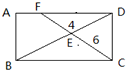 如图,BD、CF将长方形ABCD分成4块,△DEF的面积是4cm2,△CED的面积是6cm2,则四边形ABEF的面积是________平方厘米.
如图,BD、CF将长方形ABCD分成4块,△DEF的面积是4cm2,△CED的面积是6cm2,则四边形ABEF的面积是________平方厘米.