题目内容
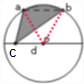
如图,直径d=4cm,ab=2cm,且与直径d平行,求阴影部分的面积.(得数保留一位小数)


考点:组合图形的面积
专题:平面图形的认识与计算
分析:本题把阴影部分的面积转化成扇形的面积进行计算,根据平行线之间的距离相等,求出三角形abc的面积等于三角形aob的面积,再通过计算三角形aob是等边三角形求出扇形圆心角的度数是60°,运用扇形的面积公式进行解答即可.
解答:
解:连接oa,ob
因为oa=ob=半径=
d=
×4=2(厘米)
ab=2厘米
所以三角形oab是等边三角形,即∠aob=60°
因为ab∥d,所以三角形abc的面积=三角形abo的面积,
所以阴影部分的面积就是半径2厘米,圆心角60°扇形的面积.
S阴影=
=
≈2.1(平方厘米)
答:阴影部分的面积是2.1平方厘米.

因为oa=ob=半径=
| 1 |
| 2 |
| 1 |
| 2 |
ab=2厘米
所以三角形oab是等边三角形,即∠aob=60°
因为ab∥d,所以三角形abc的面积=三角形abo的面积,
所以阴影部分的面积就是半径2厘米,圆心角60°扇形的面积.
S阴影=
| 60°×3.14×22 |
| 360° |
| 12.56 |
| 6 |
答:阴影部分的面积是2.1平方厘米.
点评:本题考查了扇形面积的计算,解答本题的关键是将阴影部分的面积转化为扇形OCD的面积,难度一般.

练习册系列答案
相关题目
