题目内容
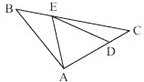 如图,BC=3BE,AC=4CD,三角形ABC的面积是三角形ADE面积的
如图,BC=3BE,AC=4CD,三角形ABC的面积是三角形ADE面积的2
2
倍.分析:由图意可知:BC=3BE,AC=4CD,则BC:BE=3:1,AC:CD=4:1,又因三角形ABE和三角形ABC,三角形CDE和三角形ACE都是等高不等底的三角形,则它们的面积比就等于对应底的比,于是即可分别得出三角形ABE和三角形CDE是三角形ABC的面积的几分之几,进而即可得出三角形ADE的面积是三角形ABC的面积的几分之几,问题即可得解.
解答:解:因为BC=3BE,AC=4CD,则BC:BE=3:1,AC:CD=4:1,
所以S△ABE=
S△ABC,S△ACE=
S△ABC,
S△ADE=
S△ACE=
×
S△ABC=
S△ABC,
三角形ABC的面积是三角形ADE面积的2倍.
故答案为:2.
所以S△ABE=
| 1 |
| 3 |
| 2 |
| 3 |
S△ADE=
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
三角形ABC的面积是三角形ADE面积的2倍.
故答案为:2.
点评:解答此题的主要依据是:等高不等底的三角形的面积比就等于对应底的比.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 已知如图长方形ABCD,F是CD的中点,BC=3BE,AD=4HD,若长方形的面积是240平方分米,则阴影部分的面积是多少平方分米?
已知如图长方形ABCD,F是CD的中点,BC=3BE,AD=4HD,若长方形的面积是240平方分米,则阴影部分的面积是多少平方分米? (2013?北京模拟)如图,有一个长方形ABCD,其中BC=3BE,AE与BD相交于F,如果三角形EBF的面积为1,那么长方形ABCD的面积为
(2013?北京模拟)如图,有一个长方形ABCD,其中BC=3BE,AE与BD相交于F,如果三角形EBF的面积为1,那么长方形ABCD的面积为 已知如图长方形ABCD,F是CD的中点,BC=3BE,AD=4HD,若长方形的面积是240平方分米,则阴影部分的面积是多少平方分米?
已知如图长方形ABCD,F是CD的中点,BC=3BE,AD=4HD,若长方形的面积是240平方分米,则阴影部分的面积是多少平方分米? 如图,有一个长方形ABCD,其中BC=3BE,AE与BD相交于F,如果三角形EBF的面积为1,那么长方形ABCD的面积为________.
如图,有一个长方形ABCD,其中BC=3BE,AE与BD相交于F,如果三角形EBF的面积为1,那么长方形ABCD的面积为________.