题目内容
 已知如图长方形ABCD,F是CD的中点,BC=3BE,AD=4HD,若长方形的面积是240平方分米,则阴影部分的面积是多少平方分米?
已知如图长方形ABCD,F是CD的中点,BC=3BE,AD=4HD,若长方形的面积是240平方分米,则阴影部分的面积是多少平方分米?
解:因为长方形的面积是240平方厘米,即SABCD=BC?AB=240,
又BC=3BE,AD=4HD,
所以S△EFC= EC×FC,
EC×FC,
= ×
× BC×
BC× CD,
CD,
= BC×AB,
BC×AB,
S△ABH= ×AB×AH,
×AB×AH,
= ×AB×
×AB× AD,
AD,
= BC×AB,
BC×AB,
则S阴影=SABCD-S△EFC-S△ABH,
=BC×AB- BC×AB-
BC×AB- BC×AB,
BC×AB,
=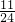 BC×AB,
BC×AB,
=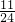 ×240,
×240,
=110(平方米);
答:阴影部分的面积是110平方分米.
分析:阴影部分的面积可由矩形的面积与△EFC、△ABH的差表示,又由题中条件可得出两个三角形面积与矩形面积的关系,进而代入数据求解即可.
点评:本题主要考查了长方形的性质及长方形、三角形面积的计算,应熟练掌握.
又BC=3BE,AD=4HD,
所以S△EFC=
 EC×FC,
EC×FC,=
 ×
× BC×
BC× CD,
CD,=
 BC×AB,
BC×AB,S△ABH=
 ×AB×AH,
×AB×AH,=
 ×AB×
×AB× AD,
AD,=
 BC×AB,
BC×AB,则S阴影=SABCD-S△EFC-S△ABH,
=BC×AB-
 BC×AB-
BC×AB- BC×AB,
BC×AB,=
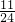 BC×AB,
BC×AB,=
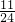 ×240,
×240,=110(平方米);
答:阴影部分的面积是110平方分米.
分析:阴影部分的面积可由矩形的面积与△EFC、△ABH的差表示,又由题中条件可得出两个三角形面积与矩形面积的关系,进而代入数据求解即可.
点评:本题主要考查了长方形的性质及长方形、三角形面积的计算,应熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012?武汉模拟)如图,已知长方形ADEF的面积是16,三角形ADB的面积是3,三角形ACF的面积是4,那么三角形ABC的面积是
(2012?武汉模拟)如图,已知长方形ADEF的面积是16,三角形ADB的面积是3,三角形ACF的面积是4,那么三角形ABC的面积是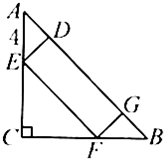 如图,△ABC是等腰直角三角形,已知AE=4cm,长方形DGFE的长DG是它的宽DE的3倍.则△ABC的面积是
如图,△ABC是等腰直角三角形,已知AE=4cm,长方形DGFE的长DG是它的宽DE的3倍.则△ABC的面积是 如图,已知ABC为扇形,BDF为扇形,CBDE为长方形.CE=8厘米,CB=10厘米求图中阴影部分的面积.
如图,已知ABC为扇形,BDF为扇形,CBDE为长方形.CE=8厘米,CB=10厘米求图中阴影部分的面积. 如图,△ABC是等腰直角三角形,已知AE=4cm,长方形DGFE的长DG是它的宽DE的3倍.则△ABC的面积是________cm2.
如图,△ABC是等腰直角三角形,已知AE=4cm,长方形DGFE的长DG是它的宽DE的3倍.则△ABC的面积是________cm2.