题目内容
在△ABC中，AE=ED，BD：CD=5：2，图中空白部分的面积是2814平方厘米，图中阴影面积是多少平方厘米？分析：此题应根据梅涅劳斯定理，得到
×
×
=1，得到
=
，设S△CEF=7X，则S△AEF=5X，S△EDC=12X，S△BED=S△ABE=30X．再由图中空白部分的面积是2814平方厘米，解决问题．
| AE |
| ED |
| DB |
| BC |
| CF |
| FA |
| CF |
| FA |
| 7 |
| 5 |
解答：解：BF截△ADC三个边，由梅涅劳斯定理得：
×
×
=1，因为BD：CD=5：2，得到
=
，
设S△CEF=7X，则S△AEF=5X，S△EDC=12X，S△BED=S△ABE=30X．
30X+12X+7X=49X=2814，
那么：X=
，
所以图中阴影面积：30X+5X=35X=35×
=2010（平方厘米）．
答：图中阴影面积是2010平方厘米．
| AE |
| ED |
| DB |
| BC |
| CF |
| FA |
| CF |
| FA |
| 7 |
| 5 |
设S△CEF=7X，则S△AEF=5X，S△EDC=12X，S△BED=S△ABE=30X．
30X+12X+7X=49X=2814，
那么：X=
| 2814 |
| 49 |
所以图中阴影面积：30X+5X=35X=35×
| 2814 |
| 49 |
答：图中阴影面积是2010平方厘米．
点评：掌握梅涅劳斯定理，是解答此题的关键．
练习册系列答案
相关题目
如图所示，在△ABC中，DC=3BD，DE=AE，若△ABC的面积是1，则△AEF的面积是
如图所示，在△ABC中，CD、AE、BF分别为BC、CA、AB长的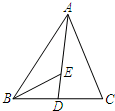
如图：在△ABC中，点D为边BC的中点，点E为线段AD上一点，且满足AE=2ED，则△ABC的面积是△BDE的面积的