题目内容
有200名学生从A地出发到相距100公里的B地,学校只有一辆限乘50人的车,为了让学生尽快到达目的地,决定采取步行与乘车相结合的办法.已知学生步行的速度是每小时5公里,汽车行驶的速度是每小时55公里,人和车同时出发,不计上下车和车掉头的时间,求最短多长时间到目的地?
考点:最大与最小
专题:综合行程问题
分析:如图:
看这个图:AB是两地距离200个人被分成4份,每组是50人,第一组直接从A开始上车被放在P1点;
汽车回到C2接到第2组放在了P2点;下面都是一样,最后一组是在C4接到的,直接送到B点; 我们知道,这4组都是同时达到B点,时间才会最短; 那么其4个组步行的距离都是一样的;当第一组被送到P1点时,回到C2点这段时间,另外三个组都步行到了C2,根据速度比=路程之比=55:5=11:1;我们把接到每组之间的步行距离看作单位1,那么汽车从出发到返回P2就是11个点; 那么出发点A到P1就是(11+1)÷2=6个点; 因为步行的距离相等,所以2段对称;(例如第一组:步行的距离是P1到B点3份,最后一组是A到C4也是三段距离是3份); 所以以第一组为研究,那么它步行了后面的3份,乘车行了前面的6份,可见全程被分为9份,每份是100÷9=
千米,步行速度是5千米,时间就是 (3×
)÷5=
小时; 乘车速度是55千米,时间就是 (6×
)÷55=
小时; 合计就是7
小时.

看这个图:AB是两地距离200个人被分成4份,每组是50人,第一组直接从A开始上车被放在P1点;
汽车回到C2接到第2组放在了P2点;下面都是一样,最后一组是在C4接到的,直接送到B点; 我们知道,这4组都是同时达到B点,时间才会最短; 那么其4个组步行的距离都是一样的;当第一组被送到P1点时,回到C2点这段时间,另外三个组都步行到了C2,根据速度比=路程之比=55:5=11:1;我们把接到每组之间的步行距离看作单位1,那么汽车从出发到返回P2就是11个点; 那么出发点A到P1就是(11+1)÷2=6个点; 因为步行的距离相等,所以2段对称;(例如第一组:步行的距离是P1到B点3份,最后一组是A到C4也是三段距离是3份); 所以以第一组为研究,那么它步行了后面的3份,乘车行了前面的6份,可见全程被分为9份,每份是100÷9=
| 100 |
| 9 |
| 100 |
| 9 |
| 20 |
| 3 |
| 100 |
| 9 |
| 40 |
| 33 |
| 29 |
| 33 |
解答:
解:(100÷9)×3÷5+(100÷9)×6÷55
=
+
=7
(小时)
答:最短7
小时到目的地.
=
| 20 |
| 3 |
| 40 |
| 33 |
=7
| 29 |
| 33 |
答:最短7
| 29 |
| 33 |
点评:此题较复杂,应抓住每组学生同时到达这个关键问题思路,进而分析解答即可.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
长方形的长与平行四边形的底相等,它们的面积也相等,那么它们的周长相比较( )
| A、长方形的周长长 |
| B、平行四边形的周长长 |
| C、相等 |
| D、无法比较 |
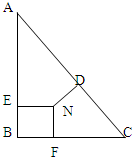 如图在直角三角形ABC中,AB⊥BC,ND⊥AC,NE⊥AB,NF⊥BC.四边形BFNE是正方形,AB=4,BC=3,AC=5,ND=1,则正方形BFNE的边长等于
如图在直角三角形ABC中,AB⊥BC,ND⊥AC,NE⊥AB,NF⊥BC.四边形BFNE是正方形,AB=4,BC=3,AC=5,ND=1,则正方形BFNE的边长等于 如图,在三角形ABC中,AB、AC两边分别被分成五等份.阴影部分的面积与空白部分的面积比是
如图,在三角形ABC中,AB、AC两边分别被分成五等份.阴影部分的面积与空白部分的面积比是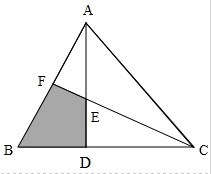 已知△ABC的面积为24cm2,D为BC中点,E为AD中点,求阴影部分面积.
已知△ABC的面积为24cm2,D为BC中点,E为AD中点,求阴影部分面积.