题目内容
用1，2，3，4，5，6，7，8这八个数字组成两个不同的四位数（每个数字只用一次）使他们的差最小，那么这个差是 ．
考点：最大与最小
专题：计算问题（巧算速算）
分析：设这两个数为a，b．，且a＜b．千位最小差只能是1．为了让差尽量小，只能使a其它位数最大，b的其它位数最小．所以要尽量使a的百位大于b的百位，a的十位大于b的十位，a的个位大于b的个位．因此分别是8和1，7和2，6和3，剩下的4，5分给千位．据此解答．
解答：
解：设这两个数为a，b．，且a＜b．千位最小差只能是1．根据以上分析，应为：
5123-4876=247
故答案为：247．
5123-4876=247
故答案为：247．
点评：此题也可这样解答：
两个四位数，差尽可能小，设较大的一个为abcd，另一个为efgh，要使差尽可能小，则a和e的差应最小，为1，a-e=1的组合有很多，因此考虑百位的b和f，要让efgh接近abcd，因此f要尽可能大，b要尽可能小，所以b=1．f=8，同理在剩下的6个数中，g要尽可能大，c要尽可能小，所以g=7，c=2，在剩下的4个数中，h要尽可能大，d要尽可能小，所以h=6，d=3，剩下4和5，正好满足a=5，e=4，a-e=5-4=1，因此两个四位数分别为5123和4876．
两个四位数，差尽可能小，设较大的一个为abcd，另一个为efgh，要使差尽可能小，则a和e的差应最小，为1，a-e=1的组合有很多，因此考虑百位的b和f，要让efgh接近abcd，因此f要尽可能大，b要尽可能小，所以b=1．f=8，同理在剩下的6个数中，g要尽可能大，c要尽可能小，所以g=7，c=2，在剩下的4个数中，h要尽可能大，d要尽可能小，所以h=6，d=3，剩下4和5，正好满足a=5，e=4，a-e=5-4=1，因此两个四位数分别为5123和4876．
练习册系列答案
相关题目
如图，有两个可旋转标有从0到5的刻度盘．现在，两个刻度盘都在0的位置．同时掷大小两个骰子，按照下面的顺序旋转刻度盘．
将1?6分别填入图中的6个方框内，使得同一行中左边的数比右边的小，同一列中上边的数比下边的小，共有
一只兔子沿着方格的边从A到B，规定上只能往上或往右走，但是必须经过一座独木桥MN，这只兔子有
变为数字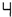
，我们必须改变3个发光体，即F、C这二个发光体由亮变暗，E这个发光体由暗变亮．