题目内容
一个两位数除以它的各位数字之和，余数最大是多少？
考点：带余除法
专题：余数问题
分析：首先设两位数为ab=10a+b，则它除以它的各位数字之和为：
，因为余数小于除数，所以要使余数大，就应使分母a+b足够大；然后分类讨论，求出余数最大是多少即可．
| 10a+b |
| a+b |
解答：
解：设两位数为ab=10a+b，
则它除以它的各位数字之和为：
，
因为余数小于除数，
所以要使余数大，就应使分母a+b足够大，
（1）a+b最大为18，a=b=9，这个两位数是99，
99÷18=5…9，余数是9，
（2）当a+b=17时，这个两位数是89或98，
89÷17=5…4，余数是4，
98÷17=5…13，余数是13，
（3）当a+b=16时，这个两位数是79或97，
79÷16=4…15，余数是15，
97÷16=6…1，余数是1，
综上，可得当这个两位数是79时，余数最大是15．
答：当这个两位数是79时，余数最大是15．
则它除以它的各位数字之和为：
| 10a+b |
| a+b |
因为余数小于除数，
所以要使余数大，就应使分母a+b足够大，
（1）a+b最大为18，a=b=9，这个两位数是99，
99÷18=5…9，余数是9，
（2）当a+b=17时，这个两位数是89或98，
89÷17=5…4，余数是4，
98÷17=5…13，余数是13，
（3）当a+b=16时，这个两位数是79或97，
79÷16=4…15，余数是15，
97÷16=6…1，余数是1，
综上，可得当这个两位数是79时，余数最大是15．
答：当这个两位数是79时，余数最大是15．
点评：此题主要考查了带余除法的性质的应用，以及分类讨论思想的应用，解答此题的关键是要明确：除法计算中，余数小于除数．
练习册系列答案
相关题目
在图中，圆的面积和长方形面积相等．俩图形重叠部分占这个长方形面积的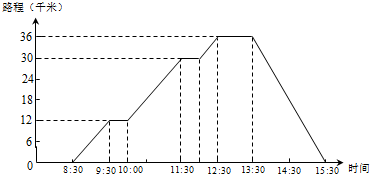
周末李艳和朋友从家出发骑车到红格去玩，请根据统计图回答问题．