题目内容
有11个人围成一个圆圈,并依次编成1~11号,从1号起依次发《趣味数学》书,发书的方法是:隔1人发1本,隔2人发1本;再隔1人发1本,隔2人发1本;再隔1人发1本,隔2人发1本….这样发下去,试问最少要准备多少本书才能使发给每人的本数同样多?
分析:第一个周期:从1号起,3号和6号各得一本,共发书2本;第二个周期:从6号起,8号和11号各得一本,共发书2本;依此类推,每个周期共发书2本;设发给每人的本数同样多都是N本,经过了M个周期,则得关系式:M=11N÷2;根据M必须是整数,即N=2、4、6、8、10、…进而得出N最小为2;问题的解.
解答:解:发给每人的本数同样多都是N本,一共需要11N本书;经过了M个周期,
所以可得,M=
,因为M必须是整数,则N=2、4、6、8、10、…(偶数);
所以要使准备的本书最少,N的值只能是2,
则总本数最少是:11×2=22(本);
答:最少要准备22本书才能使发给每人的本数同样多.
所以可得,M=
| 11N |
| 2 |
所以要使准备的本书最少,N的值只能是2,
则总本数最少是:11×2=22(本);
答:最少要准备22本书才能使发给每人的本数同样多.
点评:本题在找到每个循环周期共发书2本这个规律的基础上;得出周期数和总本书之间的关系式是解答的关键,确定N的取值范围是难点.

练习册系列答案
相关题目
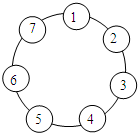 有7名同学编成1号到7号,他们依次围成一个圆圈做游戏,现在从1号开始发一本书,接下来隔两个人,即数到第4号发一本书,这样依次发下去,若有2005本书,最后一本应该发给多少号?
有7名同学编成1号到7号,他们依次围成一个圆圈做游戏,现在从1号开始发一本书,接下来隔两个人,即数到第4号发一本书,这样依次发下去,若有2005本书,最后一本应该发给多少号? 十个人围成一个圆圈,每人选择一个整数并告诉他的两个邻座的人,然后每个人算出并宣布他两个邻座所选数的平均数,这些平均数如图所示,则宣布6的那个人选择的数是
十个人围成一个圆圈,每人选择一个整数并告诉他的两个邻座的人,然后每个人算出并宣布他两个邻座所选数的平均数,这些平均数如图所示,则宣布6的那个人选择的数是