题目内容
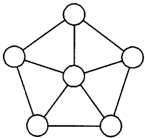 如图,在6个圆圈中填入2、3、5、7、11、13各一次,并在每个小三角形的中心处写下它3个顶点上3个数的和.那么这些三角形中心处所写数的和被3除的余数是
如图,在6个圆圈中填入2、3、5、7、11、13各一次,并在每个小三角形的中心处写下它3个顶点上3个数的和.那么这些三角形中心处所写数的和被3除的余数是1
1
.这个总合一共有6
6
种不同的可能.分析:总和的不同是由中心数字的不同所决定的,因为本题中有6个不同的数字,所以就有6种不同的可能.因为求总和时每个数字用的次数是:中心数字一共用了5次,其它数字每个用了2次;这样可以求出6个数字都用2次的和:(2+3+5+7+11+13)×2=82,然后分别用这6个数字的3倍加上82,得到的和去除以3,即可得出余数.
解答:解:(2+3+5+7+11+13)×2,
=41×2,
=82;
(1)若中心数为2,则(82+2×3)÷3=29…1;
(2)若中心数为3,则(82+3×3)÷3=30…1;
(3)若中心数为5,则(82+5×3)÷3=32…1;
(4)若中心数为7,则(82+7×3)÷3=34…1;
(5)若中心数为11,则(82+11×3)÷3=38…1;
(1)若中心数为13,则(82+13×3)÷3=40…1;
所以这6种情况的余数都是1.
故答案为:1、6.
=41×2,
=82;
(1)若中心数为2,则(82+2×3)÷3=29…1;
(2)若中心数为3,则(82+3×3)÷3=30…1;
(3)若中心数为5,则(82+5×3)÷3=32…1;
(4)若中心数为7,则(82+7×3)÷3=34…1;
(5)若中心数为11,则(82+11×3)÷3=38…1;
(1)若中心数为13,则(82+13×3)÷3=40…1;
所以这6种情况的余数都是1.
故答案为:1、6.
点评:本题重点是:要找出题中每个数字在求和中所用的次数,然后求出6个数字都用2次的和,最后根据中心数去确定问题的答案.

练习册系列答案
相关题目
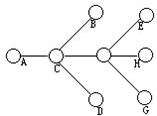 在如图中所示的小圆圈内,试分别填入1、2、3、4、5、6、7、8这八个数字,使得图中用线段连接的两个小圆圈内所填的数字之差(大数字减小数字)恰好是1、2、3、4、5、6、7这七个数字.
在如图中所示的小圆圈内,试分别填入1、2、3、4、5、6、7、8这八个数字,使得图中用线段连接的两个小圆圈内所填的数字之差(大数字减小数字)恰好是1、2、3、4、5、6、7这七个数字.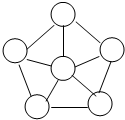 如图:5个小三角形的顶点处有6个圆圈,如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形三个顶点上的数之和相等,问这6个质数的积是多少?
如图:5个小三角形的顶点处有6个圆圈,如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形三个顶点上的数之和相等,问这6个质数的积是多少?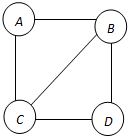 将0~5这6个数字中的4个数字填入如图的圆圈中,每条线段两端的数字作差(大减小),可以得到5个差,这5个差恰好为1-5,在所有满足条件的填法中,四位数的最大值是
将0~5这6个数字中的4个数字填入如图的圆圈中,每条线段两端的数字作差(大减小),可以得到5个差,这5个差恰好为1-5,在所有满足条件的填法中,四位数的最大值是 如图1中的圆圈内填的是6个不同的自然数,而且每个数都是上一行相邻两数之和.请按此规律,在如图2中的圆圈内填不同的自然数.
如图1中的圆圈内填的是6个不同的自然数,而且每个数都是上一行相邻两数之和.请按此规律,在如图2中的圆圈内填不同的自然数.