题目内容
已知一个等差数列的前15项之和为450，前20项之和为750，请问：这个数列的公差是多少？首项是多少？
考点：等差数列
专题：传统应用题专题
分析：想求公差，公差=（第n项-第m项）÷（n-m），如果已知这个数列的任意两项那么公差就可以求了．根据中项定理：前15项之和为450，可推出第8项为450÷15=30，前20项之和为750，第16项到20项之和为750-450=300，可推出第18项为300÷5=60，依此求出这个数列的公差，进一步求出首项．
解答：
解：450÷15=30
750-450=300
300÷5=60
（60-30）÷（18-8）
=30÷10
=3
30-（8-1）×3
=30-21
=9．
答：这个数列的公差是3，首项是9．
750-450=300
300÷5=60
（60-30）÷（18-8）
=30÷10
=3
30-（8-1）×3
=30-21
=9．
答：这个数列的公差是3，首项是9．
点评：本题考查了公差公式，及首项公式，注意题中给出了前20项之和，而20是偶数，不能直接用中项公式，依此想到求第16项到20项之和，进而求出第18项，这是本题的难点．
练习册系列答案
相关题目
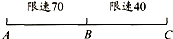如图，A与B、B与C之间的公路长度相等，且每段公路上都有限速标志（单位：千米/时）．甲货车从A出发，乙货车从C出发，并且两车在A、C之间往返行驶．结果当甲车到达C后再返回到B时，乙车刚好第一次到达B．已知甲、乙两车在各段公路上均以所能达到的最快速度行驶（不会超过车子本身的最高时速，也不能超过公路上的最高限速），且甲车的最高时速是乙车的4倍，那么甲车的最高时速是多少？