题目内容
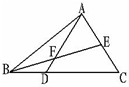 如图,三角形BAC的面积是1,E是AC的中点,点D在BC上,且BD:DC=1:2,AD与BE交于点F,则四边形DFEC的面积等于
如图,三角形BAC的面积是1,E是AC的中点,点D在BC上,且BD:DC=1:2,AD与BE交于点F,则四边形DFEC的面积等于| 5 |
| 12 |
| 5 |
| 12 |
分析:此题没法直接求出四边形DFEC的面积,可以连接CF,将它转化成△CDF和△CFE,根据已知条件即可推理得出.
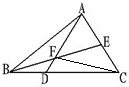

解答:解:连接CF,
设△BDF的面积为x,△CEF的面积为y,(以下△均表示其面积.)
由于E是中点,D是3分点,
所以,△BCE=△BAE=
,
2△ABD=△ADC=
,
△CEF=△EFA=y,
△DCF=2x,
△BFC=△BFA=3x,
△ABE=△BFA+△AFE,
即3x+y=
,
△ABD=△BFA+△AFE,
即3x+x=
可得:3x+y=
,3x+x=
,
所以x=
,y=
,
所以△DCF=2x=
,
四边形DEFC的面积=△DCF+△CEF=
+
=
,
答:四边形DEFC的面积是
.
故答案为:
.
设△BDF的面积为x,△CEF的面积为y,(以下△均表示其面积.)
由于E是中点,D是3分点,
所以,△BCE=△BAE=
| 1 |
| 2 |
2△ABD=△ADC=
| 2 |
| 3 |
△CEF=△EFA=y,
△DCF=2x,
△BFC=△BFA=3x,
△ABE=△BFA+△AFE,
即3x+y=
| 1 |
| 2 |
△ABD=△BFA+△AFE,
即3x+x=
| 1 |
| 3 |
可得:3x+y=
| 1 |
| 2 |
| 1 |
| 3 |
所以x=
| 1 |
| 12 |
| 3 |
| 12 |
所以△DCF=2x=
| 2 |
| 12 |
四边形DEFC的面积=△DCF+△CEF=
| 2 |
| 12 |
| 3 |
| 12 |
| 5 |
| 12 |
答:四边形DEFC的面积是
| 5 |
| 12 |
故答案为:
| 5 |
| 12 |
点评:利用已知的中点和3分点,在图形中转化要求图形的面积,是解决本题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 三角形ABC的一条高将∠BAC分成角度为42°和36°的两个角(如图).∠2和∠3分别是多少度?
三角形ABC的一条高将∠BAC分成角度为42°和36°的两个角(如图).∠2和∠3分别是多少度? 如图,三角形ABC是等腰三角形,并且∠BAC=36°,求:∠ACD的度数.
如图,三角形ABC是等腰三角形,并且∠BAC=36°,求:∠ACD的度数.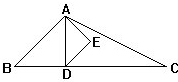 如图三角形ABC是等腰三角形.AB=AC,BAC=120°.三角形ADE是正三角形,点D在BC边上,BD:DC=2:3.当三角形ABC的面积是50cm2时,三角形ADE的面积是多少?
如图三角形ABC是等腰三角形.AB=AC,BAC=120°.三角形ADE是正三角形,点D在BC边上,BD:DC=2:3.当三角形ABC的面积是50cm2时,三角形ADE的面积是多少? 如图,△ABD△ACD都是等腰三角形,AB=BD,AD=DC,∠B和∠ADC分别是它们的顶角,又∠B=40°,那么∠BAC的度数是
如图,△ABD△ACD都是等腰三角形,AB=BD,AD=DC,∠B和∠ADC分别是它们的顶角,又∠B=40°,那么∠BAC的度数是