题目内容
 如图,△ABD△ACD都是等腰三角形,AB=BD,AD=DC,∠B和∠ADC分别是它们的顶角,又∠B=40°,那么∠BAC的度数是
如图,△ABD△ACD都是等腰三角形,AB=BD,AD=DC,∠B和∠ADC分别是它们的顶角,又∠B=40°,那么∠BAC的度数是分析:因为,△ABD是等腰三角形,AB=BD,所以∠BAD=∠BDA,因为∠B=40°,所以∠BAD=∠BDA=(180°-40°)÷2=70°,又因为∠BDA+∠ADC=180°,所以∠ADC=180°-70°=110°,因为△ACD是等腰三角形,AD=DC,所以∠C=∠DAC,所以∠C=(180°-110°)÷2=35°;在三角形ABC中,∠B=40°,∠C=35°,根据三角形的内角和是180°,由此即可求出∠BAC的度数.
解答:解:△ABD是等腰三角形,AB=BD,所以∠BAD=∠BDA,因为∠B=40°,
所以∠BAD=∠BDA=(180°-40°)÷2=70°,
又因为∠BDA+∠ADC=180°,所以∠ADC=180°-70°=110°,
因为△ACD是等腰三角形,AD=DC,所以∠C=∠DAC,
所以∠C=(180°-110°)÷2=35°;
在三角形ABC中,∠B=40°,∠C=35°,
∠BAC=180°-40°-35°=105°.
故答案为:105°.
所以∠BAD=∠BDA=(180°-40°)÷2=70°,
又因为∠BDA+∠ADC=180°,所以∠ADC=180°-70°=110°,
因为△ACD是等腰三角形,AD=DC,所以∠C=∠DAC,
所以∠C=(180°-110°)÷2=35°;
在三角形ABC中,∠B=40°,∠C=35°,
∠BAC=180°-40°-35°=105°.
故答案为:105°.
点评:本题考查了三角形的内角和定理,三角形的外角性质,等腰三角形的性质等知识,此题难度适中,解题的关键是掌握数形结合思想与方程思想的应用.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD交于点O,如果三角形ABD的面积等于三角形BCD面积的
如图,四边形ABCD的对角线AC与BD交于点O,如果三角形ABD的面积等于三角形BCD面积的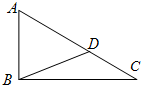 如图,直角三角形ABC中,∠ABC=90°,∠ACB=30°,点D在AC上,如果∠ADB=45°,那么∠ABD=
如图,直角三角形ABC中,∠ABC=90°,∠ACB=30°,点D在AC上,如果∠ADB=45°,那么∠ABD= 如图,若△ABC中,AB=AC,∠BAC=40°,以AB为边,在△ABC的外部作等边△ABD,∠ADC是
如图,若△ABC中,AB=AC,∠BAC=40°,以AB为边,在△ABC的外部作等边△ABD,∠ADC是 以下给出的四个语句中,结论正确的有( )
以下给出的四个语句中,结论正确的有( ) 如图,直角三角形ABC中,∠ABC=90°,∠ACB=30°,点D在AC上,如果∠ADB=45°,那么∠ABD=________度.
如图,直角三角形ABC中,∠ABC=90°,∠ACB=30°,点D在AC上,如果∠ADB=45°,那么∠ABD=________度.