20.设椭圆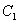 、抛物线
、抛物线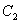 的焦点的焦点均在x轴上,中心(顶点)均为原点,从每条曲线上至少取2个点,将其坐标记录于下表中:
的焦点的焦点均在x轴上,中心(顶点)均为原点,从每条曲线上至少取2个点,将其坐标记录于下表中:
|
x |
3 |
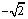 |
-2 |
4 |
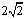 |
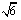 |
|
y |
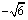 |
0 |
2 |
 |
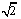 |
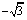 |
(1)表格中恰有一个点的坐标记录错误,它不属于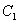 、
、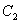 中的任何一个,指出是哪一个并说明理由;
中的任何一个,指出是哪一个并说明理由;
(2)求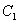 、
、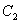 的标准方程;
的标准方程;
(3)设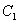 的焦点为
的焦点为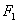 、
、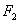 ,M为
,M为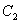 上任意一个动点,求证:
上任意一个动点,求证: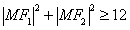
17.已知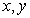 之间的一组数据如下表:
之间的一组数据如下表:
|
x |
1 |
3 |
6 |
7 |
8 |
|
y |
1 |
2 |
3 |
4 |
5 |
(1)从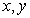 中各取一个数,求
中各取一个数,求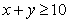 的概率;
的概率;
(2)对于表中的数据,甲、乙两同学给出的拟合直线分别为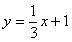 与
与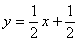 ,试利用“最小平方法(也称最小二乘法)”判断哪条直线的拟合程度更好.
,试利用“最小平方法(也称最小二乘法)”判断哪条直线的拟合程度更好.
11.(1)教育局督学组到学校检查工作,需在学号为0001-1000的高三年级的学生中抽调20人参加学校管理的综合座谈会;(2)该校高三年级这1000名学生参加2009年新年晚会,要产生20名“幸运之星”;(3)该校高三年级1000名学生一摸考试的数学成绩有240人在120分以上(包括120分),600人在120分以下90分以上(包括90分),其余在90分以下,现欲从中抽取20人研讨进一步改进数学教与学的座谈会. 用如下三种抽样方法:①简单随机抽样 ②系统抽样 ③分层抽样 选取样本,则以上三件事,最合理的抽样方法序号依次为 .
12.如图,是根据所输入的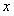 值计算
值计算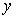 值的一个算法程序,
值的一个算法程序,
|
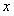 依次取数列
依次取数列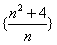 (
(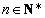 )的项,
)的项,
则所得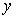 值中的最小值为
.
值中的最小值为
.
13.设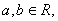 且
且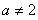 ,若定义在区间
,若定义在区间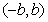 内的函数
内的函数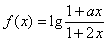 是奇函数,则
是奇函数,则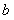 的取值范围是
.
的取值范围是
.
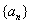 的首项
的首项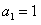 ,公差
,公差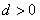 ,且第二项、第五项、第十四项分别是等比数列
,且第二项、第五项、第十四项分别是等比数列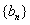 的第二项、第三项、第四项.
的第二项、第三项、第四项.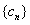 对任意的
对任意的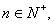 均有
均有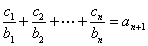 成立,求
成立,求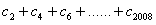 的值.
的值. 如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,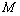 是
是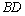 的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.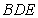 ? 若存在,确定点N的位置;
? 若存在,确定点N的位置;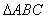 中,已知内角
中,已知内角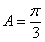 ,边BC=
,边BC=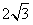 ,设内角
,设内角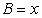 ,周长为
,周长为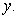
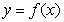 的解析式和定义域;
的解析式和定义域;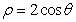 的圆心的极坐标是 ,它与方程
的圆心的极坐标是 ,它与方程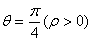 所表示的图形的交点的极坐标是
.
所表示的图形的交点的极坐标是
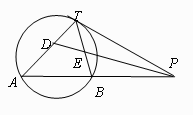
. 是⊙
是⊙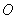 的切线,切点为
的切线,切点为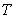 ,直线
,直线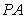 与⊙
与⊙ 两点,
两点, 的平分线分别交直线
的平分线分别交直线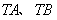 于
于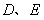 两点,已知
两点,已知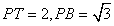 ,则
,则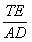 =
.
=
.
 THEN
THEN

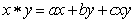 ,其中a、b、c是常数,等式右边的运算是通常的加法和乘法运算.现已知
,其中a、b、c是常数,等式右边的运算是通常的加法和乘法运算.现已知 ,并且有一个非零实数m,使得对于任意实数x,都有
,并且有一个非零实数m,使得对于任意实数x,都有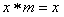 ,则m的值是( ).
,则m的值是( ).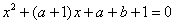 的两个实根为
的两个实根为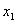 和
和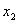 ,若有
,若有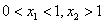 ,则
,则 的取值范围是( )
的取值范围是( )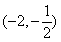 B.
B.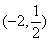 C.
C.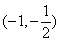 D.
D.
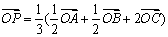 ,则点P一定为
,则点P一定为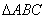 的( )
的( )