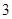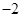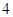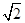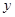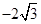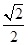摘要:20.设椭圆.抛物线的焦点的焦点均在x轴上.中心均为原点.从每条曲线上至少取2个点.将其坐标记录于下表中: x 3 -2 4 y 0 2 (1)表格中恰有一个点的坐标记录错误.它不属于.中的任何一个.指出是哪一个并说明理由, (2)求.的标准方程, (3)设的焦点为..M为上任意一个动点.求证:
网址:http://m.1010jiajiao.com/timu_id_4402780[举报]
设椭圆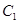 与抛物线
与抛物线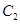 的焦点均在
的焦点均在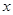 轴上,
轴上,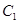 的中心及
的中心及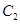 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)求曲线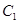 、
、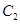 的标准方程;
的标准方程;
(Ⅱ)设直线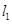 过抛物线
过抛物线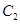 的焦点
的焦点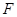 ,
,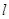 与椭圆交于不同的两点
与椭圆交于不同的两点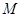 、
、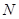 ,当
,当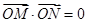 时,求直线
时,求直线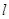 的方程.
的方程.
查看习题详情和答案>>
设椭圆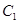 与抛物线
与抛物线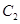 的焦点均在
的焦点均在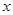 轴上,
轴上,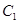 的中心及
的中心及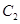 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
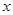 |  | 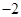 |  | 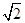 |
 | 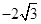 |  | 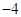 | 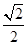 |
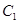 、
、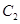 的标准方程;
的标准方程;(Ⅱ)设直线
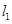 过抛物线
过抛物线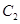 的焦点
的焦点 ,
,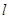 与椭圆交于不同的两点
与椭圆交于不同的两点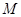 、
、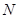 ,当
,当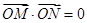 时,求直线
时,求直线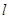 的方程.
查看习题详情和答案>>
的方程.
查看习题详情和答案>>
设椭圆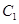 与抛物线
与抛物线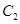 的焦点均在
的焦点均在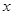 轴上,
轴上,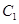 的中心及
的中心及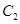 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
(Ⅰ)求曲线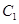 、
、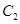 的标准方程;
的标准方程;
(Ⅱ)设直线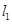 过抛物线
过抛物线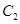 的焦点
的焦点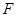 ,
,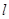 与椭圆交于不同的两点
与椭圆交于不同的两点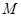 、
、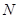 ,当
,当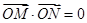 时,求直线
时,求直线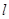 的方程.
的方程.
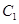 与抛物线
与抛物线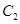 的焦点均在
的焦点均在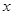 轴上,
轴上,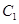 的中心及
的中心及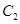 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表: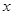 | 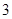 | 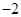 | 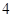 | 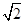 |
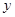 | 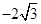 |  | 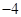 | 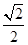 |
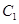 、
、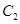 的标准方程;
的标准方程;(Ⅱ)设直线
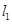 过抛物线
过抛物线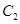 的焦点
的焦点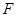 ,
,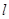 与椭圆交于不同的两点
与椭圆交于不同的两点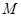 、
、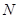 ,当
,当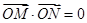 时,求直线
时,求直线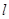 的方程.
的方程.设椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于表中:
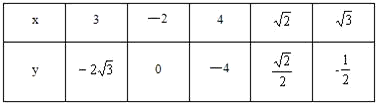
(1)求C1、C2的标准方程;
(2)设直线l与椭圆C1交于不同两点M、N,且 ,请问是否存在这样的直线l过抛物线C2的焦点F?若存在,求出直线l的方程;若不存在,说明理由.
,请问是否存在这样的直线l过抛物线C2的焦点F?若存在,求出直线l的方程;若不存在,说明理由.
查看习题详情和答案>>
设椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于表中:
(1)求C1、C2的标准方程;
(2)设直线l与椭圆C1交于不同两点M、N,且 ,请问是否存在这样的直线l过抛物线C2的焦点F?若存在,求出直线l的方程;若不存在,说明理由.
,请问是否存在这样的直线l过抛物线C2的焦点F?若存在,求出直线l的方程;若不存在,说明理由.
查看习题详情和答案>>
| x | 3 | -2 | 4 |  |  |
| y | -2 | 0 | -4 |  | - |
(2)设直线l与椭圆C1交于不同两点M、N,且
 ,请问是否存在这样的直线l过抛物线C2的焦点F?若存在,求出直线l的方程;若不存在,说明理由.
,请问是否存在这样的直线l过抛物线C2的焦点F?若存在,求出直线l的方程;若不存在,说明理由.查看习题详情和答案>>