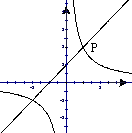
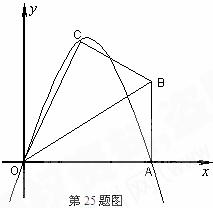
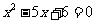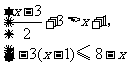25.(本题满分12分)已知:在Rt△ABO中,∠OAB=90°,∠BOA=30°,AB=2,若以O为坐标原点,OA所在直线为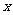 轴,建立如图所示平面直角坐标系,点B在第一象限内,将Rt△ABO沿OB折叠后,点A落在第一象限内的点C处.
轴,建立如图所示平面直角坐标系,点B在第一象限内,将Rt△ABO沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;(3分)
(2)若抛物线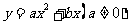 经过C、A两点,求此抛物线的解析式;(4分)
经过C、A两点,求此抛物线的解析式;(4分)
(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作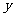 轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. (5分)
轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. (5分)
|
[答案]25.(1)过点C作CH⊥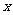 轴,垂足为H, ∵在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2 ∴OB=4,OA=
轴,垂足为H, ∵在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2 ∴OB=4,OA=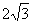 ,由折叠知,∠COB=300,OC=OA=
,由折叠知,∠COB=300,OC=OA=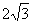
∴∠COH=600,OH=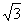 ,CH=3 ∴C点坐标为(
,CH=3 ∴C点坐标为(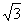 ,3)
,3)
(2)∵抛物线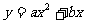 (
(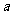 ≠0)经过C(
≠0)经过C(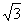 ,3)、A(
,3)、A(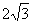 ,0)两点
,0)两点
∴ 解得:
解得: 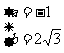
∴此抛物线的解析式为: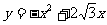
(3)存在. 因为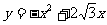 的顶点坐标为(
的顶点坐标为(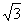 ,3)即为点C,MP⊥
,3)即为点C,MP⊥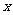 轴,设垂足为N,PN=
轴,设垂足为N,PN=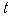 ,因为∠BOA=300,所以ON=
,因为∠BOA=300,所以ON=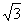
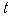 , ∴P(
, ∴P(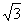
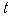 ,
,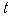 )
)
作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E,把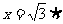 代入
代入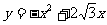 得:
得: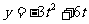 ,∴ M(
,∴ M(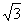
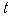 ,
,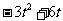 ),E(
),E(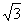 ,
,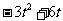 ) 同理:Q(
) 同理:Q(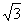 ,
,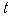 ),D(
),D(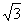 ,1), 要使四边形CDPM为等腰梯形,只需CE=QD
,1), 要使四边形CDPM为等腰梯形,只需CE=QD
即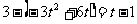 ,解得:
,解得: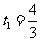 ,
,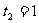 (舍), ∴ P点坐标为(
(舍), ∴ P点坐标为(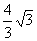 ,
,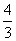 )
)
∴ 存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐为(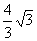 ,
,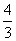 )
)

|

|
版权所有:()
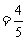 ,EC=2,
,EC=2,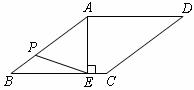
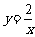 的图象在第一象限的交点为P(t ,2) 。
的图象在第一象限的交点为P(t ,2) 。