反函数的定义
一般地,设函数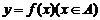 的值域是C,根据这个函数中x,y 的关系,用y把x表示出,得到x=
的值域是C,根据这个函数中x,y 的关系,用y把x表示出,得到x= (y). 若对于y在C中的任何一个值,通过x=
(y). 若对于y在C中的任何一个值,通过x= (y),x在A中都有唯一的值和它对应,那么,x=
(y),x在A中都有唯一的值和它对应,那么,x= (y)就表示y是自变量,x是自变量y的函数,这样的函数x=
(y)就表示y是自变量,x是自变量y的函数,这样的函数x=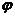 (y) (y
(y) (y C)叫做函数
C)叫做函数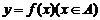 的反函数,记作
的反函数,记作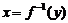 ,习惯上改写成
,习惯上改写成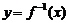
开始的两个例子:s=vt记为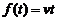 ,则它的反函数就可以写为
,则它的反函数就可以写为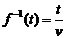 ,同样
,同样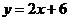 记为
记为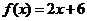 ,则它的反函数为:
,则它的反函数为: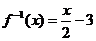 .
.
探讨1:所有函数都有反函数吗?为什么?
反函数也是函数,因为它符合函数的定义,从反函数的定义可知,对于任意一个函数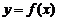 来说,不一定有反函数,如
来说,不一定有反函数,如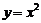 ,只有“一一映射”确定的函数才有反函数,
,只有“一一映射”确定的函数才有反函数,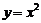 ,
,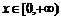 有反函数是
有反函数是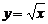
探讨2:互为反函数定义域、值域的关系
从映射的定义可知,函数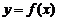 是定义域A到值域C的映射,而它的反函数
是定义域A到值域C的映射,而它的反函数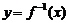 是集合C到集合A的映射,因此,函数
是集合C到集合A的映射,因此,函数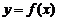 的定义域正好是它的反函数
的定义域正好是它的反函数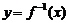 的值域;函数
的值域;函数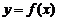 的值域正好是它的反函数
的值域正好是它的反函数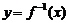 的定义域
的定义域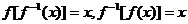 (如下表):
(如下表):
|
|
函数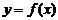 |
反函数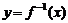 |
|
定义域 |
A |
C |
|
值 域 |
C |
A |
探讨3: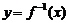 的反函数是?
的反函数是?
若函数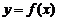 有反函数
有反函数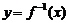 ,那么函数
,那么函数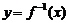 的反函数就是
的反函数就是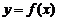 ,这就是说,函数
,这就是说,函数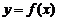 与
与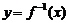 互为反函数
互为反函数
 ,从A到B的映射f满足
,从A到B的映射f满足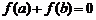 ,那么这样的映射
,那么这样的映射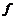
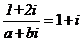 ,则
,则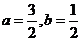 B.
B. 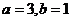 C.
C. 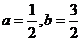
 D.
D. 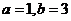
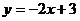 (x∈R) (2)
(x∈R) (2)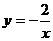 (x∈R,且x≠0)
(x∈R,且x≠0)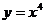 (x≥0) (4)
(x≥0) (4)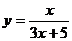 (x∈R,且x≠
(x∈R,且x≠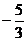 )
)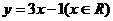 ;
②
;
②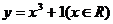 ;
;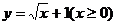 ; ④
; ④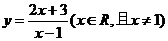 .
.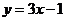 解得
解得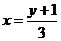
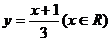 ,
,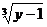 ,
,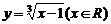
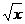 +1解得x=
+1解得x= ,
, 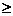 0,∴y
0,∴y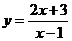 解得
解得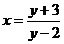
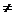 1},∴y
1},∴y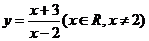
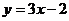 (
(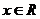 )的反函数,并画出原来的函数和它的反函数的图像
)的反函数,并画出原来的函数和它的反函数的图像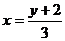
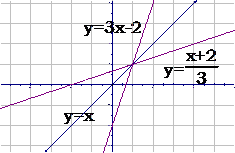 ∴函数
∴函数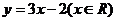 的反函数是
的反函数是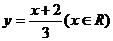 ,
,
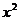 <1 ∴0<1 -
<1 ∴0<1 -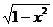 < 1 ∴0 < y <1
< 1 ∴0 < y <1 (∵ -1< x < 0 )
(∵ -1< x < 0 )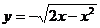 (0<x<1 )
(0<x<1 )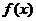 =
= 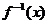 .
.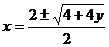 ,
,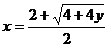 ,即x=1+
,即x=1+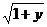 --①,
--①, 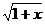 (x≥0,x∈R);
(x≥0,x∈R);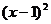 -1,∴
-1,∴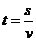 ,这时,位移s是自变量,时间t是位移s的函数,定义域s
,这时,位移s是自变量,时间t是位移s的函数,定义域s 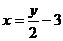 . 这样,对于y在R中任何一个值,通过式子
. 这样,对于y在R中任何一个值,通过式子