20.(16分)已知定点C(-1,0)及椭圆x2+3y2=5,过点C的动直线与椭圆相交于A,B两点.
(1)若线段AB中点的横坐标是-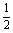 ,求直线AB的方程;
,求直线AB的方程;
(2)在x轴上是否存在点M,使 ·
· 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.
解 (1)依题意,直线AB的斜率存在,设直线AB的方程为y=k(x+1),
将y=k(x+1)代入x2+3y2=5,
消去y整理得(3k2+1)x2+6k2x+3k2-5=0.
设A(x1,y1),B(x2,y2),
|

由线段AB中点的横坐标是-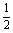 ,
,
得 =-
=- =-
=-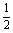 ,解得k=±
,解得k=± ,适合①.
,适合①.
所以直线AB的方程为x-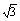 y+1=0,或x+
y+1=0,或x+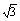 y+1=0.
y+1=0.
(2)假设在x轴上存在点M(m,0),使 ·
· 为常数.
为常数.
(ⅰ)当直线AB与x轴不垂直时,由(1)知
x1+x2=- ,x1x2=
,x1x2= .
③
.
③
所以 ·
· =(x1-m)(x2-m)+y1y2
=(x1-m)(x2-m)+y1y2
=(x1-m)(x2-m)+k2(x1+1)(x2+1)
=(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2.
将③代入,整理得
 ·
· =
= +m2
+m2
= +m2
+m2
=m2+2m-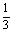 -
- .
.
注意到 ·
· 是与k无关的常数,从而有
是与k无关的常数,从而有
6m+14=0,m=- ,此时
,此时 ·
· =
= .
.
(ⅱ)当直线AB与x轴垂直时,
此时点A,B的坐标分别为
 、
、 ,
,
当m=- 时,亦有
时,亦有 ·
· =
= .
.
综上,在x轴上存在定点M ,使
,使 ·
· 为常数.
为常数.
 2Ag+(aq) + CrO2-4(aq)
2Ag+(aq) + CrO2-4(aq)
 5Ca2++3PO43-+OH-
进食后,细菌和酶作用于食物,产生有机酸,这时牙齿就会受到腐蚀,其原因是
已知Ca5(PO4)3F(固)的溶解度比上面的矿化产物更小,质地更坚固。主动脉用离子方程式表示,当牙膏中配有氟化物添加剂后能防止龋齿的原因:
5Ca2++3PO43-+OH-
进食后,细菌和酶作用于食物,产生有机酸,这时牙齿就会受到腐蚀,其原因是
已知Ca5(PO4)3F(固)的溶解度比上面的矿化产物更小,质地更坚固。主动脉用离子方程式表示,当牙膏中配有氟化物添加剂后能防止龋齿的原因:



 Ca2++2
Ca2++2 ,CaCO3(固)
,CaCO3(固)  。在火力发电厂燃烧煤的废气中往往含有SO2、O2、N2,CO2等,为了除去有害气体SO2变废为宝,常常见粉末状的碳酸钙或熟石灰的悬浊液洗涤废气,反应产物为石膏
。在火力发电厂燃烧煤的废气中往往含有SO2、O2、N2,CO2等,为了除去有害气体SO2变废为宝,常常见粉末状的碳酸钙或熟石灰的悬浊液洗涤废气,反应产物为石膏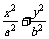 =1 (a>b>0)的左、右焦点分别为F1、F2.F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
=1 (a>b>0)的左、右焦点分别为F1、F2.F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|= .
. =
= +
+ ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若 ·
· =0,求直线l的方程.
=0,求直线l的方程. ,y1=
,y1= .所以M
.所以M .
.
 .
. =
=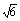 .
. 消去y并整理得
消去y并整理得 ,x1x2=
,x1x2= .
. -6m·
-6m· (14m2-28)=0.
(14m2-28)=0.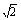 .此时Δ=(16m)2-4×9(8m2-4)>0.
.此时Δ=(16m)2-4×9(8m2-4)>0.