摘要:理.20)在直角坐标系xOy中,椭圆C1: =1 的左.右焦点分别为F1.F2.F2也是抛物线C2:y2=4x的焦点.点M为C1与C2在第一象限的交点.且|MF2|=. (1)求C1的方程, (2)平面上的点N满足=+.直线l∥MN.且与C1交于A.B两点.若·=0.求直线l的方程. 解 (1)由C2:y2=4x,知F2(1,0), 设M(x1,y1),M在C2上, 因为|MF2|=,所以x1+1=, 得x1=,y1=.所以M. M在C1上,且椭圆C1的半焦距c=1, 于是 消去b2并整理得9a4-37a2+4=0. 解得a=2(a=不合题意,舍去). 故b2=4-1=3. 故椭圆C1的方程为. (2)由=+,知四边形MF1NF2是平行四边形,其中心为坐标原点O, 因为l∥MN,所以l与OM的斜率相同. 故l的斜率k==. 设l的方程为y=(x-m). 由消去y并整理得 9x2-16mx+8m2-4=0. 设A(x1,y1),B(x2,y2), 则x1+x2=,x1x2=. 因为⊥,所以x1x2+y1y2=0. 所以x1x2+y1y2=x1x2+6(x1-m)(x2-m) =7x1x2-6m(x1+x2)+6m2 =7·-6m·+6m2 =(14m2-28)=0. 所以m=±.此时Δ=(16m)2-4×9(8m2-4)>0. 故所求直线l的方程为y=x-2,或y=x+2.
网址:http://m.1010jiajiao.com/timu_id_4006021[举报]
19、在2008年北京奥运会羽毛球女单决赛中,中国运动员张宁以2:1力克排名世界第一的队友谢杏芳,蝉联奥运会女单冠军.羽毛球比赛按“三局二胜制”的规则进行(即先胜两局的选手获胜,比赛结束),且各局之间互不影响.根据两人以往的交战成绩分析,谢杏芳在前两局的比赛中每局获胜的概率是0.6,但张宁在前二局成1:1的情况下,在第三局中凭借过硬的心理素质,获胜的概率为0.6.若张宁与谢杏芳下次在比赛上相遇.
(1)求张宁以2:1获胜的概率;
(2)设张宁的净胜局数为ξ,求ξ的分布列及Eξ.
查看习题详情和答案>>
(1)求张宁以2:1获胜的概率;
(2)设张宁的净胜局数为ξ,求ξ的分布列及Eξ.
 =(0,-1,1),
=(0,-1,1),  =(4,1,0),|λ
=(4,1,0),|λ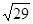 ,且λ>0,则λ=________________.
,且λ>0,则λ=________________.