2．从中文到英文

第17回“后院墙下忽开一隙，得泉一脉，开沟仅尺许，灌入墙内，绕阶缘屋至前院，盘旋竹下而出。”

我们看这句《红楼梦》里的中文，第一小句8个字，中间小句4、5、4个字，结尾7、6个字，流水句，节奏感好，情景清新明快，画面感强，是典型的优美的中文。

我们看看英文翻译：

“A stream gushed through an opening at the foot of the garden wall into a channel barely a foot wide which ran to the foot of the rear terrace and thence round the side of the house to the front， where it meandered through the bamboos of the forecourt before finally disappearing through another opening in the surrounding wall.”

我突出句中的逗号，是为了让大家看清楚这是英文的一个大长句。这个英文长句，很气派，前半句竟然有40个词，后半句有19个词，蔚为大观，就像一列火车，呼啦啦拽起了那么多的车厢，轰然前行。中文习惯于短句子，读写听说，我们都会有这样的感觉，短句子会让我们更加便利，更加舒服。如果说英文是一列长长的火车，那么中文呢，就像个手推车，一人一车，翻山越岭，细步款款。

1．从英文到中文

有这么一段英文：

Soon they had finished their tea and sat down to a collection of choice wine and delicacies.

上面这段英文翻译成中文，可以翻译成：他们很快喝完了茶，然后，坐下来尽享美食佳肴。--这样的中文译文，应该说是基本合格的。但是，实际上，这句英文是《红楼梦》一句话的翻译结果。我们看看曹雪芹的原话是什么：

须臾茶毕，早已设下杯盘，那美酒佳肴自不必说。(第八回)

上面这段英文是标准的英文，上下文衔接连贯，句式紧凑，而曹雪芹的原文呢，无疑是非常好的中文，是流水句式，生动鲜活，比起“基本合格”的中文来说，有天壤之别！

Step I Pre-reading

Ask the students to get ready for reading by discussing about some infectious diseases and the ways of making a scientific research.

Step II Reading

Let the students read through the whole passage and finish the required task.

Help them to have a better understanding of the article by providing some background information and analysis.

Step III Post-reading

Hold a discussion after reading in order to widen students’ views and further consolidate their knowledge on the topic.

Homework: Finish the reading passage in the workbook.

Communicative Approach, Task-based Approach

　　 a. Understand the spirit of science and scientists.

b. Understand the details of each stage in examining a new scientific idea.

c. Discuss what attitude the scientists should take towards a complete new finding that is against the present theory.

2、　 知识目标(Knowledge Aims)

To lead the students to get some information on the steps of a scientific research through reading.

　　 Reading part in students’ book

1、　 能力目标(Ability Aims)

To train the students’ ability in skimming & scanning.

To adapt the scientific spirit in their pursuit of knowledge.

21.(Ⅰ)解：当a=1时，f(x)=，f(2)=3；f’(x)=, f’(2)=6.所以曲线y=f(x)在点(2，f(2))处的切线方程为y-3=6(x-2)，即y=6x-9.

(Ⅱ)解：f’(x)=.令f’(x)=0，解得x=0或x=.

以下分两种情况讨论：

(1)　　　 若，当x变化时，f’(x)，f(x)的变化情况如下表：

X		0
f’(x)	+	0	-
f(x)		极大值

　　 当等价于

　　 解不等式组得-5<a<5.因此.

(2)　　　 若a>2，则.当x变化时，f’(x),f(x)的变化情况如下表：

X		0
f’(x)	+	0	-	0	+
f(x)		极大值		极小值

当时，f(x)>0等价于即

解不等式组得或.因此2<a<5.

综合(1)和(2)，可知a的取值范围为0<a<5.

20.I)当时，汽车从甲地到乙地行驶了小时，

　　 要耗没(升)。

　　 答：当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地耗油17.5升。

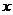　　 (II)当速度为千米/小时时，汽车从甲地到乙地行驶了小时，设耗油量为升，

　　 依题意得

　　 令得当时，是减函数；

　　 当时，是增函数。　 当时，取到极小值　 因为在上只有一个极值，所以它是最小值。

答：汽车以80千米/小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为11.25升