摘要：如图 ,椭圆的中心在原点, 焦点在x轴上, 过其右焦点F作斜率为1的直线, 交椭圆于A.B两点, 若椭圆上存在一点C, 使+＝. 若＝15, 求着个椭圆的方程. 解: (1)设椭圆的方程为, 焦距为, 则直线l的方程为:, 代入椭圆方程, 得, 设点., 则 ∵+, ∴C点坐标为. ∵C点在椭圆上, ∴.∴ ∴ 又∴∴ (2) ∵ 由已知从而. ∴.故椭圆的方程为: .
网址：http://m.1010jiajiao.com/timu_id_4393929[举报]
,求椭圆的离心率.
如图,椭圆的中心为原点O,长轴在x轴上,离心率e=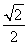
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
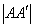=4.
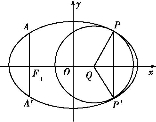
(1)求该椭圆的标准方程;
(2)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP′Q的面积S的最大值,并写出对应的圆Q的标准方程.
查看习题详情和答案>>
如图,椭圆的中心为原点O,长轴在x轴上,离心率e=
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
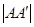=4.
(1)求该椭圆的标准方程;
(2)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP′Q的面积S的最大值,并写出对应的圆Q的标准方程.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
=4.
如图，已知中心在原点0、焦点在x轴上的椭圆T过点M（2，1），离心率为