题目内容
如图,椭圆的中心在原点,焦点在x轴上,过右焦点F作斜率为1的直线交椭圆于A、B两点,若椭圆上存在一点C,使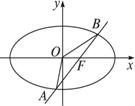
解:设椭圆方程为![]() =1(a>b>0),F(c,0),
=1(a>b>0),F(c,0),
由 得(a2+b2)x2-2a2cx+a2c2-a2b2=0.
得(a2+b2)x2-2a2cx+a2c2-a2b2=0.
设A(x1,y1),B(x2,y2),∴x1+x2=![]() ,y1+y2=x1+x2-2c=
,y1+y2=x1+x2-2c=![]() .
.
∵![]() +
+![]() =
=![]() ,∴C点坐标是(
,∴C点坐标是(![]() ,
,![]() ).
).
C点在椭圆上,即![]() +
+![]() =1,∴
=1,∴![]() =1.
=1.
又c2+b2=a2,∴5c2=2a2.∴椭圆离心率e=![]() .
.

练习册系列答案
相关题目
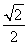
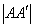
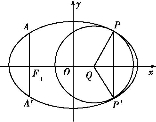
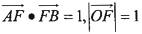 .
. ,直线l1与椭圆分别交于点M,N,直线l2与椭圆分别交于点P,Q,且
,直线l1与椭圆分别交于点M,N,直线l2与椭圆分别交于点P,Q,且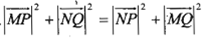 ,求四边形MPNQ的面积S的最小值.
,求四边形MPNQ的面积S的最小值.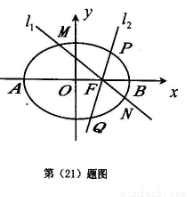
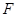 为椭圆的左焦点,
为椭圆的左焦点, 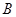 为椭圆的一个顶点,过点
为椭圆的一个顶点,过点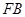 垂直的直线
垂直的直线 交
交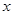 轴于
轴于 点, 且椭圆的长半轴长
点, 且椭圆的长半轴长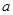 和短半轴长
和短半轴长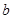 是关于
是关于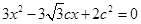 (其中
(其中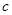 为半焦距)的两个根.
为半焦距)的两个根.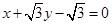 相切,试求椭圆的方程.
相切,试求椭圆的方程.
 (1)求椭圆的离心率;
(1)求椭圆的离心率;