摘要：数列的有关概念, 数列的表示方法:列举法,图象法,解析法,递推法． 与的关系:．
网址：http://m.1010jiajiao.com/timu_id_4389485[举报]
定义：在数列{an}中，若an2-an-12=p，（n≥2，n∈N*，p为常数），则称{an}为“等方差数列”．下列是对“等方差数列”的有关判断：
①若{an}是“等方差数列”，则数列{
}是等差数列；
②{（-2）n}是“等方差数列”；
③若{an}是“等方差数列”，则数列{akn}（k∈N*，k为常数）也是“等方差数列”；
④若{an}既是“等方差数列”，又是等差数列，则该数列是常数数列．
其中正确的命题为
查看习题详情和答案>>
①若{an}是“等方差数列”，则数列{
| 1 | an |
②{（-2）n}是“等方差数列”；
③若{an}是“等方差数列”，则数列{akn}（k∈N*，k为常数）也是“等方差数列”；
④若{an}既是“等方差数列”，又是等差数列，则该数列是常数数列．
其中正确的命题为
③④
③④
．（写出所有正确命题的序号）．定义：在数列
中，若
，（
，
，
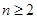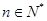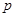为常数），则称为“等方差数列”．下列是对“等方差数列”的有关判断：
①若是“等方差数列”，则数列
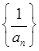是等差数列；
②
是“等方差数列”；
③若是“等方差数列”，则数列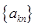
（
，
为常数）也是“等方差数列”；
④若既是“等方差数列”，又是等差数列，则该数列是常数数列．
其中正确的命题为 ．（写出所有正确命题的序号）
查看习题详情和答案>>
定义：在数列
中，若
，（n≥2，n∈N*，p为常数），则称为“等方差数列”．下列是对“等方差数列”的有关判断：
①若是“等方差数列”，则数列
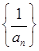是等差数列；②
是“等方差数列”；
③若是“等方差数列”，则数列（k∈N*，k为常数）也是“等方差数列”；
④若既是“等方差数列”，又是等差数列，则该数列是常数数列．
其中正确的命题为 ．（写出所有正确命题的序号）
查看习题详情和答案>>
中，若
，（n≥2，n∈N*，p为常数），则称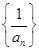
是等差数列；②
是“等方差数列”；
（k∈N*，k为常数）也是“等方差数列”；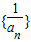
是等差数列；