摘要：§ 数列的定义, § 数列的通项公式. § 本节课的能力要求是: § 会由通项公式 求数列的特定项
网址：http://m.1010jiajiao.com/timu_id_4379126[举报]
数列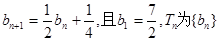
的前n项和。
（1）求证：数列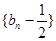
是等比数列，并求
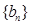的通项公式；
（2）如果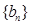对任意
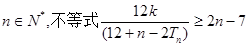恒成立，求实数k的取值范围。
【解析】本试题主要是考查了等比数列的定义的运用，以及运用递推关系求解数列通项公式的运用，并且能借助于数列的和，放缩求证不等式的综合试题。
查看习题详情和答案>>
（本小题满分12分）已知数列
，
定义其倒均数是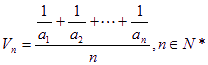
。
（1）求数列{
}的倒均数是
，求数列{}的通项公式；
（2）设等比数列
的首项为－1，公比为
，其倒数均为
，若存在正整数k，使得当
恒成立，试找出一个这样的k值（只需找出一个即可，不必证明）
（本小题满分13分）已知数列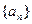
，定义其倒均数是
。
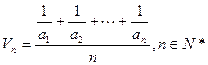（1）求数列{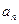
}的倒均数是
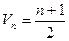，求数列{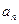}的通项公式；
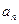（2）设等比数列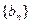
的首项为－1，公比为
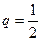，其倒数均为
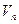，若存在正整数k，使
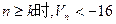恒成立，试求k的最小值。
，
。
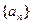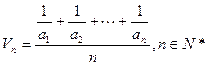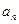}的倒均数是
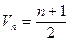，求数列{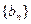
的首项为－1，公比为
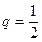，其倒数均为
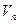，若存在正整数k，使得当
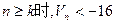恒成立，试找出一个这样的k值（只需找出一个即可，不必证明）
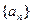，定义其倒均数是
。
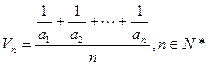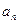}的倒均数是
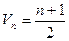，求数列{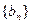
的首项为－1，公比为
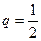，其倒数均为
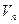，若存在正整数k，使
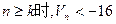恒成立，试求k的最小值。