题目内容
数列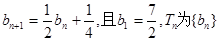
的前n项和。
（1）求证：数列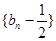
是等比数列，并求
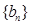的通项公式；
（2）如果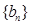对任意
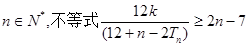恒成立，求实数k的取值范围。
【解析】本试题主要是考查了等比数列的定义的运用，以及运用递推关系求解数列通项公式的运用，并且能借助于数列的和，放缩求证不等式的综合试题。
【答案】
解: （1） 对任意
,都有
，所以
……1分
则
成等比数列,首项为
，公比为
…………2分
所以
，
…………4分
（2） 因为
所以
…………6分
因为不等式
，化简得
对任意恒成立……7分
设
，则
…………9分
当
,
,
为单调递减数列，当
,
,为单调递增数列
,所以, 
时, 
取得最大值
…………11分
所以, 要使对任意恒成立，
练习册系列答案
阳光课堂课时作业系列答案
相关题目