题目内容
(本小题满分12分)已知数列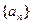 ,
,
定义其倒均数是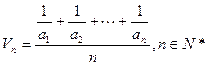 。
。
(1)求数列{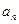 }的倒均数是
}的倒均数是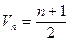 ,求数列{
,求数列{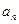 }的通项公式
}的通项公式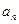 ;
;
(2)设等比数列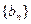 的首项为-1,公比为
的首项为-1,公比为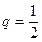 ,其倒数均为
,其倒数均为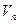 ,若存在正整数k,使得当
,若存在正整数k,使得当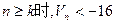 恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
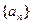 ,
,定义其倒均数是
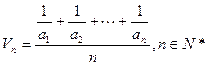 。
。(1)求数列{
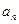 }的倒均数是
}的倒均数是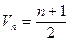 ,求数列{
,求数列{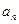 }的通项公式
}的通项公式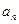 ;
;(2)设等比数列
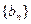 的首项为-1,公比为
的首项为-1,公比为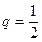 ,其倒数均为
,其倒数均为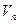 ,若存在正整数k,使得当
,若存在正整数k,使得当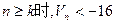 恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)(1) (2)见解析
(2)见解析
 (2)见解析
(2)见解析(1)依题意,
即
当
两式相减得,得
∴ ……………………4分
……………………4分
当n=1时,
∴ =1适合上式……………………5分
=1适合上式……………………5分
故 …………………………6分
…………………………6分
(2)由题意,
∴
 ………………10分
………………10分
不等式 恒成立,即
恒成立,即 恒成立。…………11分
恒成立。…………11分
经检验: 时均适合题意(写出一个即可)。
时均适合题意(写出一个即可)。

即

当

两式相减得,得

∴
 ……………………4分
……………………4分当n=1时,

∴
 =1适合上式……………………5分
=1适合上式……………………5分故
 …………………………6分
…………………………6分(2)由题意,

∴

 ………………10分
………………10分不等式
 恒成立,即
恒成立,即 恒成立。…………11分
恒成立。…………11分经检验:
 时均适合题意(写出一个即可)。
时均适合题意(写出一个即可)。
练习册系列答案
相关题目
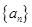 的前
的前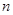 项和为
项和为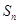 ,且
,且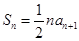 (
(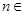 N*),其中
N*),其中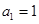 .
.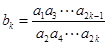 (
(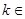 N*).
N*).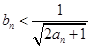 ;
;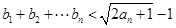 .
.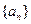 ,
,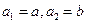 ,且对满足
,且对满足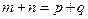 的正整数
的正整数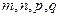 都有
都有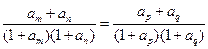 。
。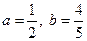 时,求通项
时,求通项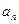 ;
;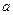 ,存在与
,存在与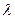 ,使得对于每个正整数
,使得对于每个正整数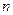 ,都有
,都有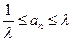 。
。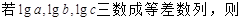 ( )
( )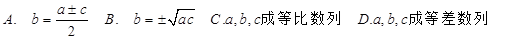
 中,有
中,有 ,则此数列的前13项之和为
,则此数列的前13项之和为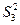 =9S2,
=9S2,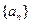 是等差数列,
是等差数列,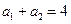 ,
,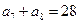 ,则该数列前10项和
,则该数列前10项和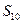 等于( )
等于( )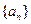 是公差不为0的等差数列,且
是公差不为0的等差数列,且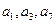 为等比数列
为等比数列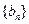 的连续三项,则数列
的连续三项,则数列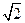
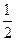
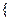
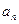
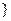 的前
的前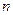 项和为
项和为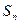 ,点列
,点列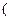
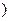 在函数
在函数
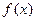 =
=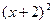 的图像上.数列
的图像上.数列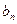
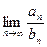 =2成立,则数列
=2成立,则数列