摘要： 第一定义 椭圆: 双曲线:
网址：http://m.1010jiajiao.com/timu_id_4373437[举报]
如图，双曲线C1：| x2 |
| 4 |
| y2 |
| b2 |
| x2 |
| 4 |
| y2 |
| b2 |
（I）求证：
| kAA1+kAA2 |
| kPA1+kPA2 |
（II）证明：△OAA2与△OA2P不相似．
（III）设满足{（x，y）|
| x2 |
| 4 |
| y2 |
| m2 |
| x2 |
| 4 |
| y2 |
| 3 |
如图，双曲线C1：
与椭圆C2：
（0＜b＜2）的左、右顶点分别为A1、A2第一象限内的点P在双曲线C1上，线段OP与椭圆C2交于点A，O为坐标原点．
（I）求证：
为定值（其中
表示直线AA1的斜率，
等意义类似）；
（II）证明：△OAA2与△OA2P不相似．
（III）设满足{（x，y）|
，x∈R，y∈R}⊆{（x，y）|
，x∈R，y∈R} 的正数m的最大值是b，求b的值．
查看习题详情和答案>>
与椭圆C2：（0＜b＜2）的左、右顶点分别为A1、A2第一象限内的点P在双曲线C1上，线段OP与椭圆C2交于点A，O为坐标原点．（I）求证：
为定值（其中表示直线AA1的斜率，等意义类似）；（II）证明：△OAA2与△OA2P不相似．
（III）设满足{（x，y）|
，x∈R，y∈R}⊆{（x，y）|，x∈R，y∈R} 的正数m的最大值是b，求b的值．
查看习题详情和答案>>
（本题满分18分，其中第1小题6分，第2小题4分，第3小题8分）
定义变换
：
可把平面直角坐标系上的点
变换到这一平面上的点
.特别地，若曲线
上一点
经变换公式变换后得到的点
与点重合，则称点是曲线在变换下的不动点.
（1）若椭圆
的中心为坐标原点，焦点在
轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2. 求该椭圆的标准方程. 并求出当
时，其两个焦点
、
经变换公式变换后得到的点
和
的坐标；
（2）当时，求（1）中的椭圆在变换下的所有不动点的坐标；
（3）试探究：中心为坐标原点、对称轴为坐标轴的双曲线在变换
：（
，
）下的不动点的存在情况和个数.
：
可把平面直角坐标系上的点
变换到这一平面上的点
.特别地，若曲线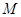
上一点
经变换公式
与点
的中心为坐标原点，焦点在
轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2. 求该椭圆
时，其两个焦点
、
经变换公式
和
的坐标；
，
）下的不动点的存在情况和个数.
：
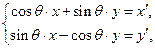可把平面直角坐标系上的点
变换到这一平面上的点
.特别地，若曲线
上一点
经变换公式
与点
的中心为坐标原点，焦点在
轴上，且焦距为
，长轴顶点和短轴顶点间的距离为2. 求该椭圆
时，其两个焦点
、
经变换公式
和
的坐标；
，
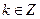）下的不动点的存在情况和个数.